Minimum area triangle encompassing two circles
Two tangent circles of radii 5 and 7 are to be inscribed in a triangle. Find the minimum area of a triangle circumscribed about the two circles.
The answer is 405.84.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
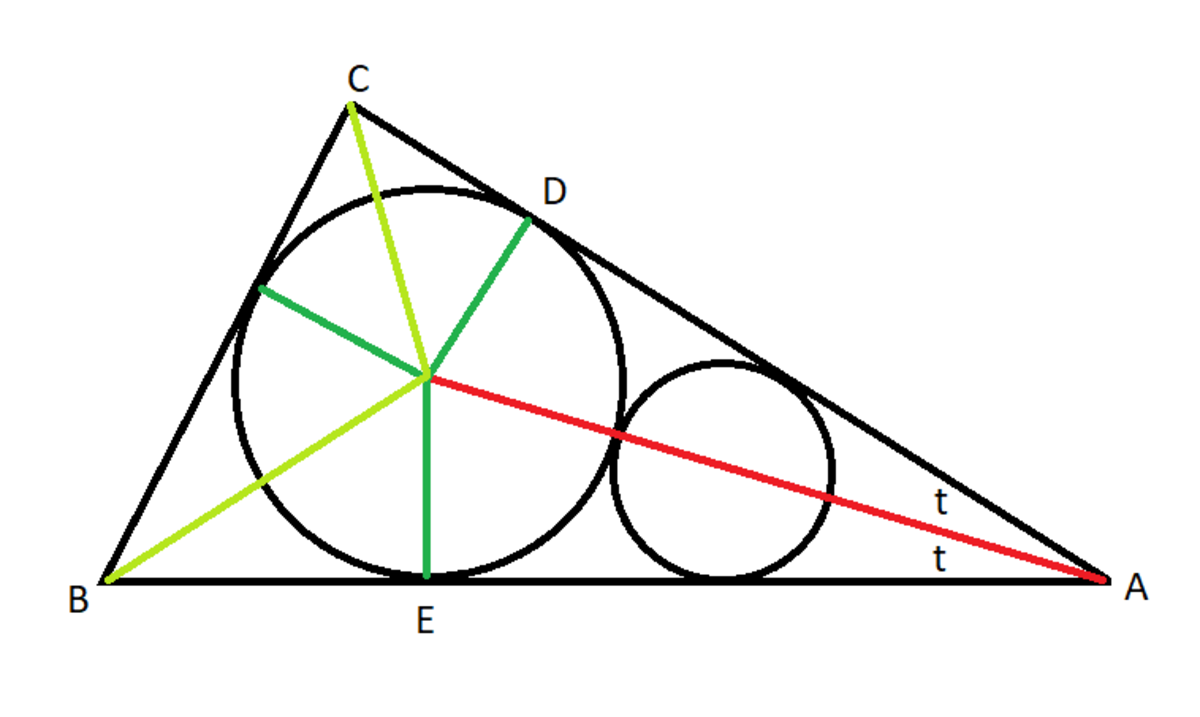
The centers of the two circles lie on the bisector of ∠ A . If t is half of ∠ A , then it is easy to show that
sin t = r 2 + r 1 r 2 − r 1 = 6 1
where r 1 = 5 , r 2 = 7 .
The length of the red line is L = r 1 + sin t r 1 + r 2 = 4 2
Next connect the center of the bigger circle to its tangency point with B C , and let the angle between this segment (green) and the extension of the red line be θ . It follows that the area of the triangle is given by
Δ = L 2 cos t sin t + r 2 2 ( tan ( 4 π + 2 1 ( t − θ ) ) + tan ( 4 π + 2 1 ( t + θ ) ) )
Differentiating the area with respect to θ :
d θ d Δ = r 2 2 ( − 2 1 sec 2 ( 4 π + 2 1 ( t − θ ) ) + 2 1 sec 2 ( 4 π + 2 1 ( t + θ ) ) )
Equating this to zero, gives us the optimal value of θ = 0 , which clearly minimizes Δ . With θ = 0 , the expression for Δ becomes
Δ = L 2 cos t sin t + 2 r 2 2 tan ( 4 π + 2 t )
Evaluating this, results in Δ ≈ 4 0 5 . 8 4 3 1
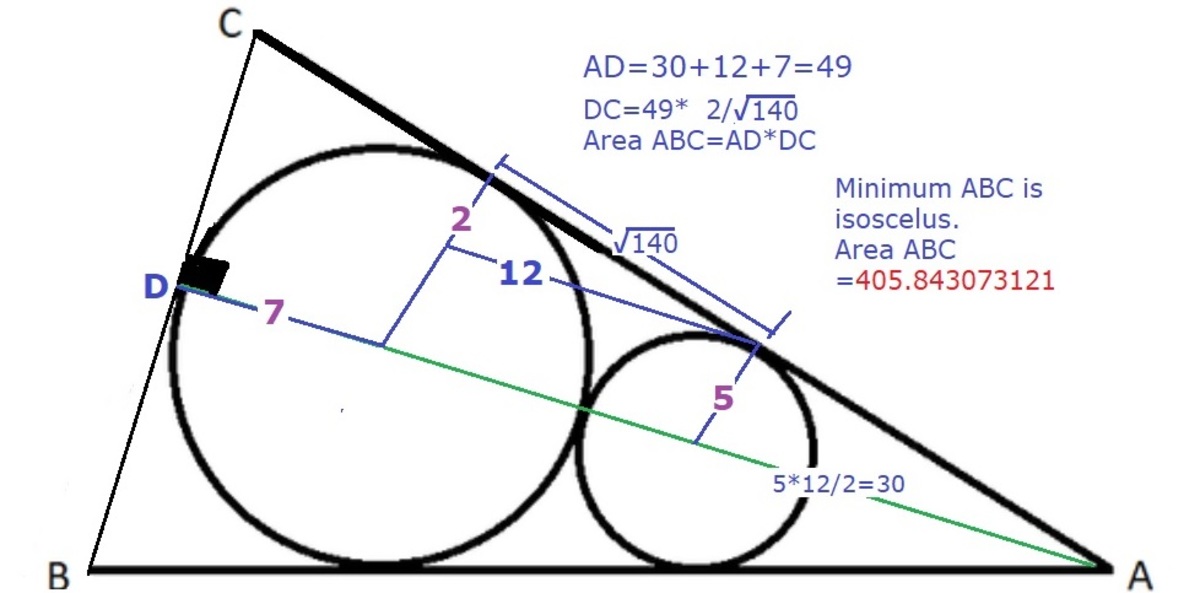
Considering the trapezium P Q H F , we know that F H = D G = 2 3 5 . By considering similar right-angled triangles, we have G B = H B = 5 3 5 .
If A E = A F = u and C D = C E = v , then the triangle A B C has area Δ and semiperimeter s , where Δ = 7 3 5 × s u v s = u + v + 7 3 5 Since the inradius of A B C is 7 we deduce that Δ = 7 s , and hence 7 s = 5 u v . It is clear that s , and hence Δ = 7 s , will be minimized when u = v = w where 5 w 2 w 2 − 2 5 7 w + 4 9 ( w − 5 7 ) 2 = 7 ( 2 w + 7 3 5 ) = 2 w 7 + 4 9 5 = 0 = 5 7 × 3 6 and hence w = 7 5 7 . Thus we deduce that the least possible area of A B C is 3 4 3 5 7 = 4 0 5 . 8 4 3 0 7 3 1 . . . .