Minimum Equilateral Triangle Inscribed in Half an Equilateral Triangle
Equilateral triangle △ A B C has side lengths of 1 4 and a median A M .
If the smallest possible equilateral triangle △ D E F is drawn such that D is on A C , E is on A M , and F is on M C , then the side lengths of △ D E F are n . Find n .
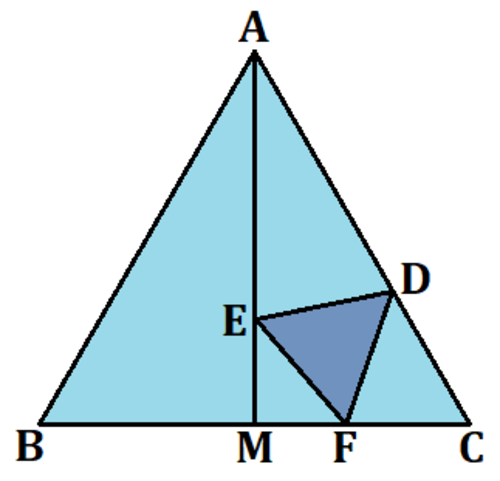
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Wow, this is very clever! Thanks for sharing.
Taking the origin of our coordinate system at point M , and if the center of △ D E F is point C = ( C x , C y ) , and its circumradius is r , and the clockwise angle that vector C D makes with the vertical direction is θ then the coordinates of points D , E , F are given by:
D = ( C x + r sin θ , C y + r cos θ )
F = ( C x + r sin ( θ + 1 2 0 ∘ ) , C y + r cos ( θ + 1 2 0 ∘ ) )
E = ( C x + r sin ( θ − 1 2 0 ∘ ) , C y + r cos ( θ − 1 2 0 ∘ ) )
Now, we know that point D lies on the line y = 7 3 − 3 x , that point F lies on the line y = 0 , and the point E lies on the line x = 0 . Hence,
C y + r cos θ = 7 3 − 3 ( C x + r sin θ )
C y + r cos ( θ + 1 2 0 ∘ ) = 0
C x + r sin ( θ − 1 2 0 ∘ ) = 0
Substituting for C y and C x from the second and third equations into the first equation, yields,
− r cos ( θ + 1 2 0 ∘ ) + r cos θ = 7 3 − 3 ( − r sin ( θ − 1 2 0 ∘ ) + r sin θ )
Collecting terms containing r , and using the formulas for the sine and the cosine of the sum and difference of angles, yields,
r ( cos θ ( − cos 1 2 0 ∘ + 1 + 3 sin 1 2 0 ∘ ) + sin θ ( sin 1 2 0 ∘ − 3 cos 1 2 0 ∘ + 3 ) ) = 7 3
Substituting cos 1 2 0 ∘ and sin 1 2 0 ∘ , the last equation becomes,
r = 3 cos θ + 2 3 sin θ 7 3
Since we want the minimum r , then we want the maximum of the denominator, which is 3 2 + ( 2 3 ) 2 = 9 + 1 2 = 2 1
Hence, the minimum circumradius is
r min = 2 1 7 3 = 7
Finally the side length of an equilateral triangle corresponding a circumradius r is s = 2 r sin 6 0 ∘ = 3 r . Thus, the required side length of the smallest possible inscribed equilateral triangle is s min = 3 7 = 2 1 , so that the answer is 2 1 .
Nice solution!
Interesting fact is that the sides of this equilateral triangle are parallel to the Napoleon's triangle. I guess it would be in general case, but I do not have a proof.
Log in to reply
That is fascinating and a great observation! I was able to prove the general case for a right angle triangle using coordinate geometry. If M is on the origin and C is at ( a , 0 ) and A is at ( b , 0 ) , then the slope of E F (and the slope of the corresponding side of the Napoleon triangle) both come out to − 3 a + 2 b a + 3 b
There are some clues here
We need the pedal triangle of X(15) which is First Isodynamic Point . It is Isogonal Conjugate of Fermat point. Using formulae for Exact Trilinear Coordinates we get α = 2 3 and γ = 3 . They are perpendicular, so n = α 2 + γ 2 = 2 1
By the properties of an equilateral triangle, C M = 7 , A M = 7 3 , cos ∠ A C M = 2 1 , and cos ∠ C A M = 2 3 .
Let x = F M , y = E M , z = A D , and s = D E = D F = E F . Then C F = 7 − x , A E = 7 3 − y , and C D = 1 4 − z .
By the law of cosines on △ C D F , △ A D E , and by Pythagorean's Theorem on △ E F M :
s 2 = ( 7 − x ) 2 + ( 1 4 − z ) 2 − 2 ⋅ ( 7 − x ) ⋅ ( 1 4 − z ) ⋅ 2 1
s 2 = ( 7 3 − y ) 2 + z 2 − 2 ⋅ ( 7 3 − x ) ⋅ z ⋅ 2 3
s 2 = x 2 + y 2
These three equations can be rearranged to s 2 = 4 7 ( x − 3 ) 2 + 2 1 , which means s 2 has a minimum of 2 1 and s has a minimum of 2 1 . Therefore, n = 2 1 .
Let the side of equilateral △ D E F be x and ∠ E F M = θ . The M C is given by:
M C 7 ⟹ x = M F + F C = x cos θ + x cos ( 1 2 0 ∘ − θ ) + x sin ( 1 2 0 ∘ − θ ) cot 6 0 ∘ = cos θ + cos ( 1 2 0 ∘ − θ ) + sin ( 1 2 0 ∘ − θ ) cot 6 0 ∘ 7 = cos θ − 2 1 cos θ + 2 3 sin θ + 2 1 cos θ + 2 3 1 sin θ 7 = cos θ + 3 2 sin θ 7 = 3 7 sin ( θ + tan − 1 2 3 ) 7 = sin ( θ + tan − 1 2 3 ) 2 1
Therefore, min ( x ) = 2 1 , when sin ( θ + tan − 1 2 3 ) = 1 . ⟹ n = 2 1 .