Minimum Length of Cart + Pure Rolling!
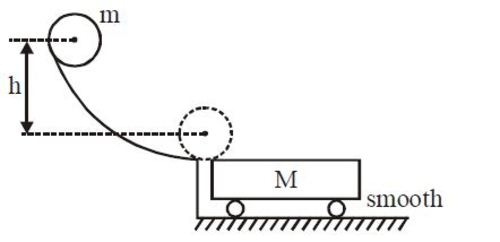 A uniform disc of mass
slides down along smooth, friction less hill, which ends in a horizontal plane without break. The disc is released from rest at a height of
(it has no initial speed and it does not rotate), and lands on the top of a cart of mass
, which can move on a friction less surface. The coefficient of kinetic friction between the cart and the disc is
. Find minimum length of the cart (in
) so that the disc begins to roll without slipping before loosing contact with the cart.
A uniform disc of mass
slides down along smooth, friction less hill, which ends in a horizontal plane without break. The disc is released from rest at a height of
(it has no initial speed and it does not rotate), and lands on the top of a cart of mass
, which can move on a friction less surface. The coefficient of kinetic friction between the cart and the disc is
. Find minimum length of the cart (in
) so that the disc begins to roll without slipping before loosing contact with the cart.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the conservation of energy velocity of m when it lands on M is 5 m / s
Now from the figure
M a = f k ............(1)
f k = 0 . 4 ( 1 2 ) g = 4 8 N
So from (1) a = 8
So the acceleration of m is m m a + f k = 1 2
Now
f k R = I α
So 8 = R α
Now using v = u + a t we get
v = 5 − 1 2 t
and ω = 8 t / R
Now for pure rolling v = R ω
So 8 t = 5 − 1 2 t So t = 0 . 2 5
So the pure rolling motion after 0 . 2 5 s e c .
As S = u t + 0 . 5 t 2
So S = 7 / 8
So the length of the plank should be greater than of equal to 7 / 8 m.