Minimum perimeter
As shown, A B C is an equilateral triangle of side length 10. The points D , E and F on B C , A B and A C respectively with D B = 2 . Let s = D E + E F + F D . Find the minimum value of ⌊ 1 0 0 s ⌋ .
The answer is 1587.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The only point pivoted for triangle DEF is D. Think of the triangle as being composed of a single thread curled across bars AB and AC. As you pull the thread harder, the perimeter reduces. As a consequence something else happens as well. The angle of incidence of thread on the bar will be equal to the angle of reflection, when the perimeter is minimum. The angles have been labled as θ and ϕ .
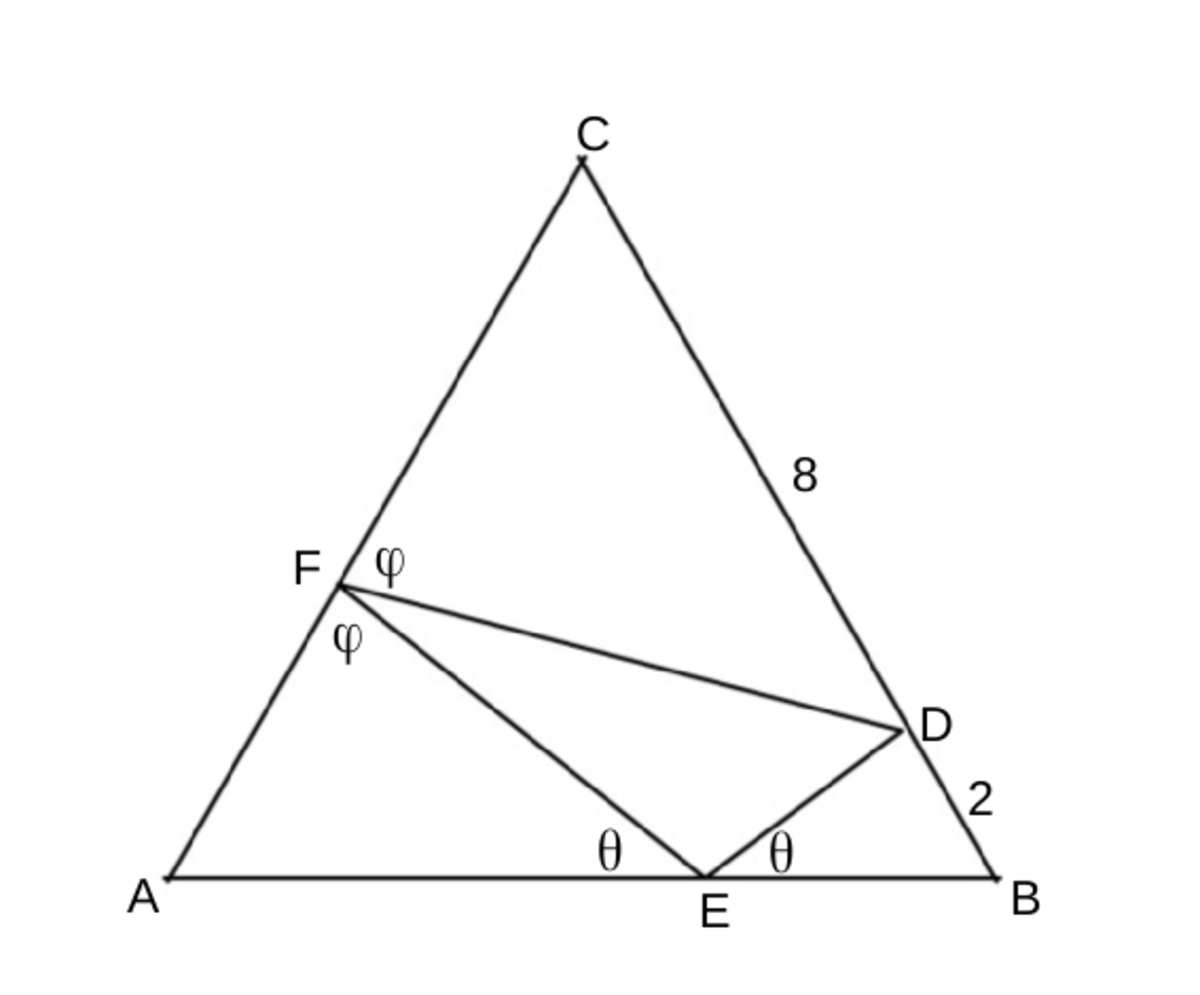
Now using the property that sum of all angles of a triangle is 1 8 0 o , we have, θ + ϕ = 1 2 0 o . The remining angles are then found in terms of θ and ϕ as shown in figure.
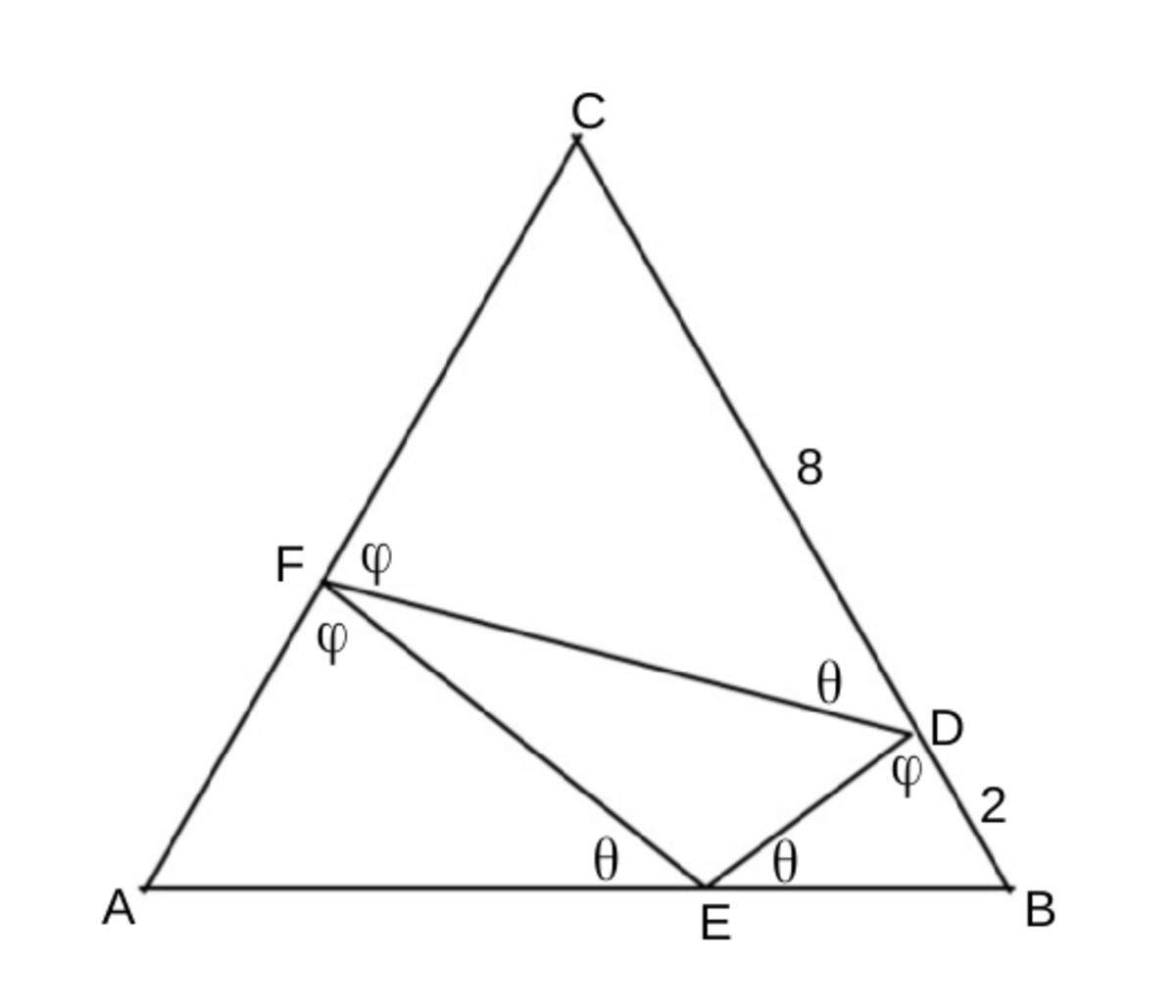
It can be seen that there are 3 similar triangles in the picture, in the following order,
CDF ~ BED ~ AEF
The sides of a normalised triangle, also similar to these triangles are assumed to be in the ratio 1 : a : b.
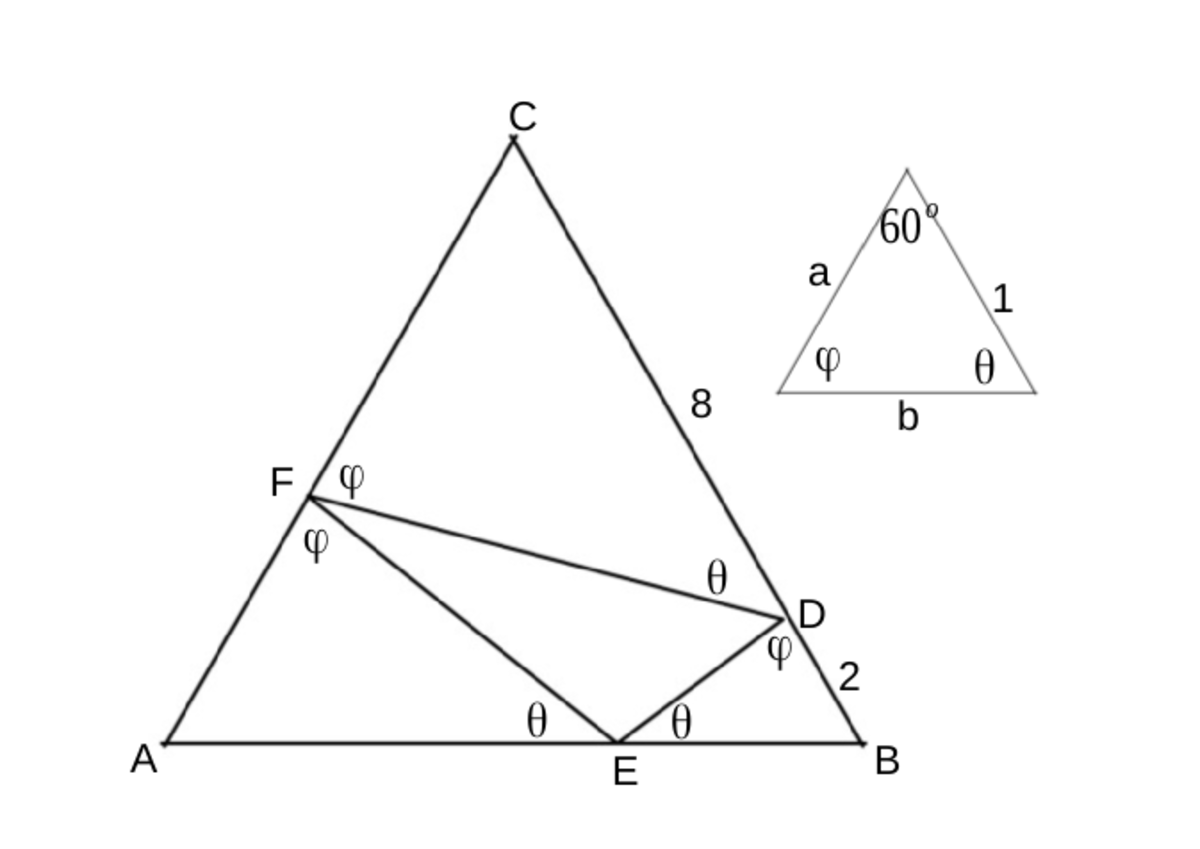
All sides in the figure can be found in terms of the assumed ratios as demonstrated,
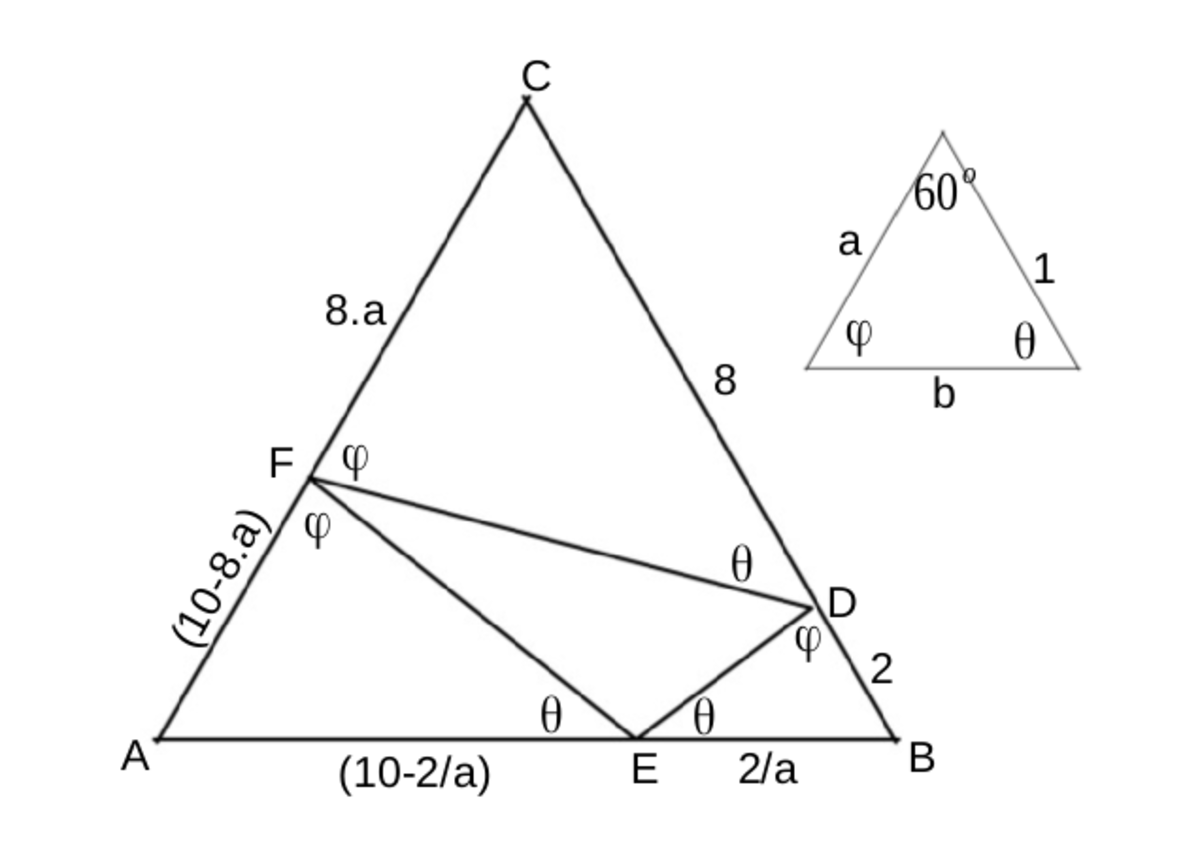
we also have, A F / A E = a from the properties of similar triangles. Substituting values of AF and AE from figure and solving, we get,
a = 2/3
To find b, cosine law is used,
b 2 = 1 2 + ( 2 / 3 ) 2 − 2 . ( 2 / 3 ) . 1 . c o s ( 6 0 o )
on solving,
b = 7 / 3
The three sides of the triangle are found to be, 3 ∗ 7 / 3 , 7 ∗ 7 / 3 , 8 ∗ 7 / 3 .
Thus, perimeter = 6 . 7
Moderator note:
Good intuition, but you should still explain why these must hold. For example, you should say "When D and E are fixed, then to minimize the distance DF+FE, we can use the reflection principle to show that the 2 angles are equal".
The reason is that you haven't fully explained why there can't be multiple local minima where the "pulled string" cannot be tightened further. For example, if the edge was a curvy line instead, then the "pulled string" analogy no longer applies.
An interesting 'physical' approach! (+1)
I did the same way.
I used the coordinate system, despite it is quite brutal and a lot of "tough" equations!
Assume that the coordinate of
A
is
(
0
,
0
)
, then the corresponding coordinates of
B
and
C
are
(
1
0
,
0
)
and
(
5
,
5
3
)
, respectively.
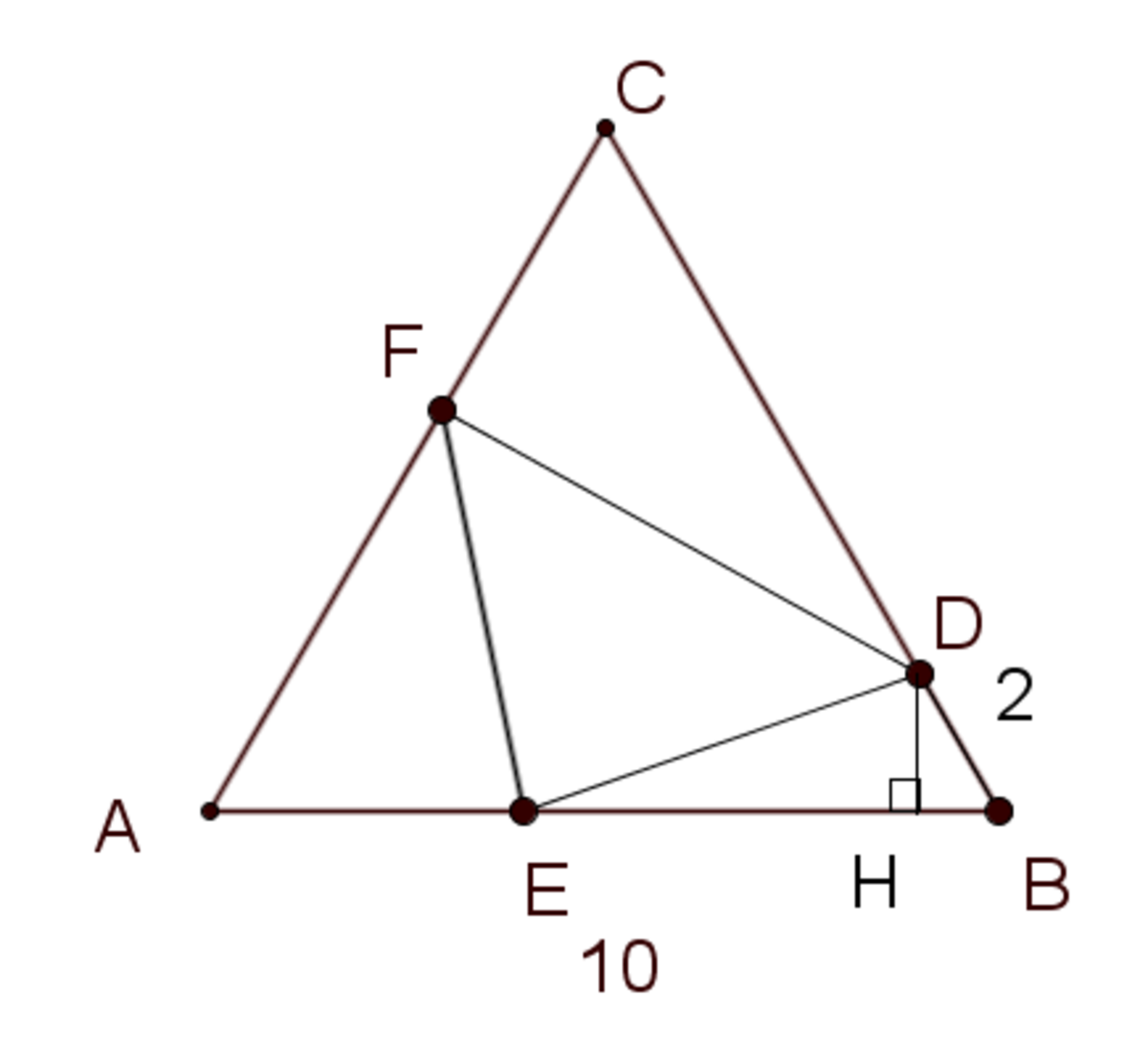
It is obvious that D H = 3 and A H = 9 (because A B = 1 0 and B H = 1 , therefore, the coordinate of D is ( 9 , 3 ) . Next, because F lies on side A C of equilateral triangle A B C , so F have a coordinate of ( m , 3 m ) , for real number m satisfies 0 < m < 5 . Beside that, the coordinate of E is ( n , 0 ) for real number n satisfies 0 < n < 1 0 .
By the distance formula:
D E = ( 9 − n ) 2 + ( 3 − 0 ) 2
D F = ( 9 − m ) 2 + ( 3 − 3 m ) 2
E F = ( n − m ) 2 + ( 0 − 3 m ) 2
So
s = D E + D F + E F = ( 9 − n ) 2 + ( 3 − 0 ) 2 + ( 9 − m ) 2 + ( 3 − 3 m ) 2 + ( n − m ) 2 + ( 0 − 3 m ) 2
We use caluclus here: Define the function f ( m , n ) = ( 9 − n ) 2 + ( 3 − 0 ) 2 + ( 9 − m ) 2 + ( 3 − 3 m ) 2 + ( n − m ) 2 + ( 0 − 3 m ) 2 .
In order to minimize the value of the function, then the partial derivatives of the function must equal zero, simultaneously:
f m ( m , n ) = 4 m 2 − 2 m n + n 2 4 m − n + m 2 − 6 m + 2 1 2 m − 6 = 0
f n ( m , n ) = 4 m 2 − 2 m n + n 2 n − m + n 2 − 1 8 n + 8 4 n − 9 = 0
Solving the above system of equations yields m = 3 7 , n = 7 , satisfy the conditions above.
Plus the recently-found values into the formula for s , then s = 6 7 . Therefore ⌊ 1 0 0 s ⌋ = ⌊ 6 0 0 7 ⌋ = ⌊ 1 5 8 7 . 4 5 0 7 8 7 . . . ⌋ = 1 5 8 7 .
Moderator note:
Do you see how to go from your equation of s , to the reflection approach used by Chan Lye Lee? Taking the geometric interpretation of these expressions often provides a more intuitive understanding.
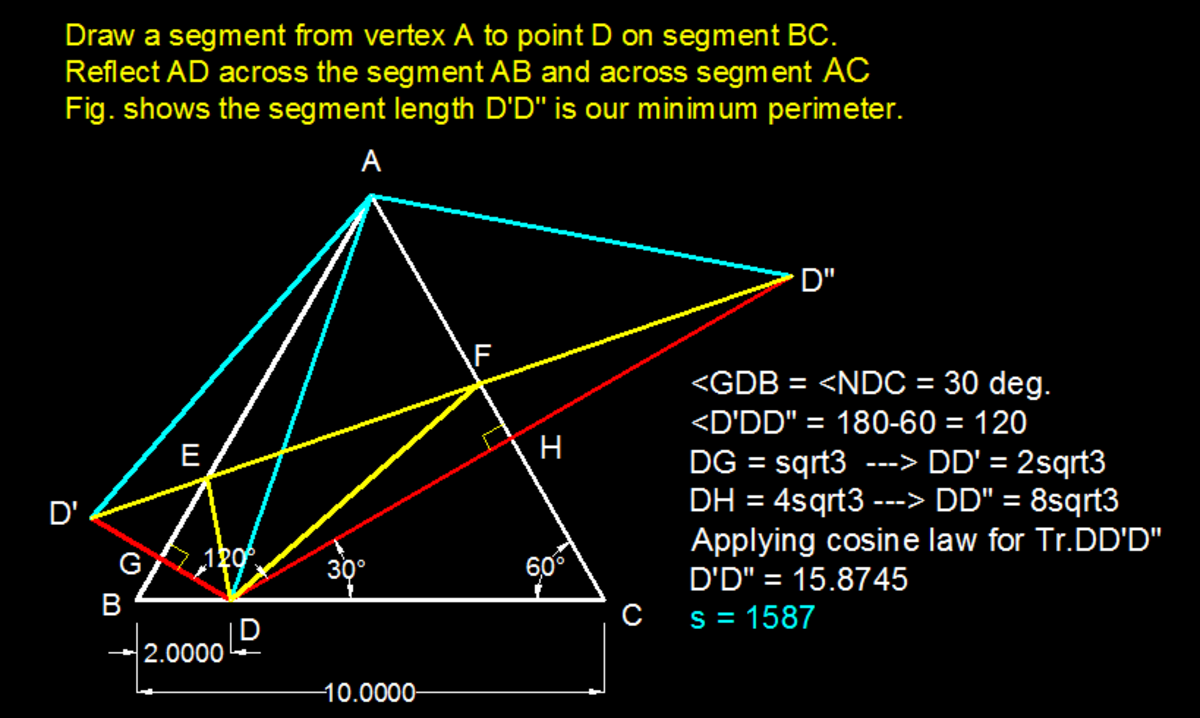
Relevant wiki: Reflection
Reflect the triangle A B C and the point D along the side A B . The reflection of D marked as D ′ . Note that D E = D ′ E .
Reflect the triangle A B C and the point D along the side A C . The reflection of D marked as D 1 ′ . Note that F D = F D 1 ′ .
Now D E + E F + F D = D ′ E + E F + F D 1 ′ , which the minimum length is clearly the same as D ′ D 1 ′ .
It is not difficult to calculate that G D ′ = 8 + 5 − 2 cos 6 0 ∘ = 1 2 and that G D 1 ′ = 1 2 sin 6 0 ∘ = 6 3 . Hence s = D ′ D 1 ′ = 6 7 and thus ⌊ 1 0 0 s ⌋ = ⌊ 6 0 0 7 ⌋ = 1 5 8 7