Minimum of a $\sin$ and $\cos$ combo

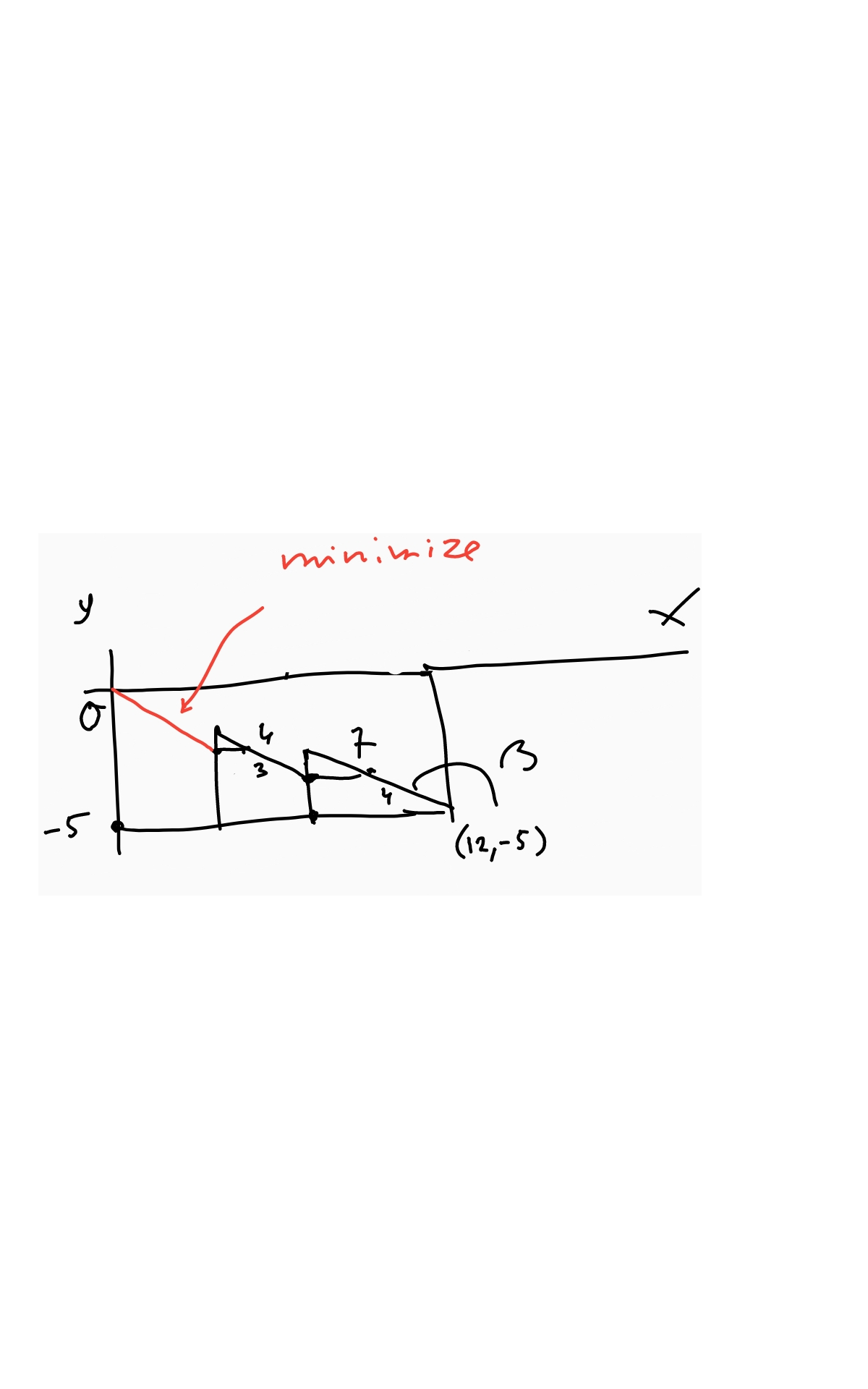
For $f(α,β)=(12+4\cos α + 7 \cos β)^2+(-5 + 3 \sin α + 4 \sin β)^2$ we derive $\frac{\partial f}{\partial α}=-8(12+4\cos α + 7 \cos β) \sin α + 6(-5 + 3 \sin α + 4 \sin β)\cos α$ $\frac{\partial f}{\partial β}=-14(12+4\cos α + 7 \cos β) \sin β + 8(-5 + 3 \sin α + 4 \sin β)\cos β$ By setting $\frac{\partial f}{\partial α}=0$ we find $8(12+4\cos α + 7 \cos β) \sin α = 6(-5 + 3 \sin α + 4 \sin β)\cos α$ so that $\tan α=\frac{\sin α}{\cos α} = \frac{3}{4}×\frac{(-5 + 3 \sin α + 4 \sin β)}{(12+4\cos α + 7 \cos β) }$ Also, by setting and $\frac{\partial f}{\partial β}=0$ $14(12+4\cos α + 7 \cos β) \sin β = 8(-5 + 3 \sin α + 4 \sin β)\cos β$ so that $\tan β =\frac{\sin β}{\cos β} = \frac{4}{7}×\frac{(-5 + 3 \sin α + 4 \sin β)}{(12+4\cos α + 7 \cos β)}$ Combining these, we find

$\tan β = \frac{16}{21} \tan α$ From a graphical representation (see below) it is clear that both α and β must be in the 2nd quadrant, so we can set $β=π+\arctan(\frac{16}{21} \tan α)$ and from there express all trig expressions in terms of α.

This way the problem reduces to its single-variable version, which greatly reduces the effort. Putting the formulas in Excel it was easy to search for a value of α for which $\frac{\partial f}{\partial α}$ was as close to 0 as possible. We find $α \approx 2.598889521$ radians, and $f(α) \approx 8.07247561$

I used simulated annealing and the function provided in the python module scipy.optimize. I have also noticed that by applying the function scipy.optimize.minimize (it only searches for a local minima), I got the same result, so the target function is not so mean .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# -*- coding: utf-8 -*-
"""
solution of:
    https://brilliant.org/problems/minimum-of-a-sin-and-cos-combo/
"""

import scipy.optimize
import numpy


def get_val(in_vec):
    """
    returns the value of the function from:
        https://brilliant.org/problems/minimum-of-a-sin-and-cos-combo/
    """
    alpha = in_vec[0]
    beta = in_vec[1]
    val_a = 12+4*numpy.cos(alpha)+7*numpy.cos(beta)
    val_b = -5+3*numpy.sin(alpha)+4*numpy.sin(beta)
    return val_a**2+val_b**2


LOWER = [0]*2
UPPER = [2*numpy.pi]*2
RES = scipy.optimize.dual_annealing(
    get_val,
    bounds=list(zip(LOWER, UPPER)),
    maxiter=10000)
print(RES.fun)