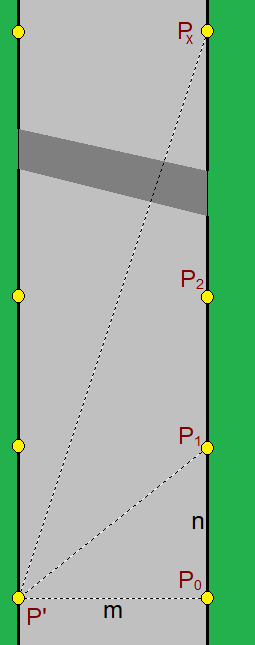
Minimum Road Width

Number Theory Level 4

A road is $m$ meters wide( $m$ is an integer),there are lampposts at both sides of the road.

The lampposts are equally spaced(space $=n$ meters, $n$ is an integer) on each side of the road.

I am standing on the east side of the road,under a lamppost $P_0$ .

There is another lamppost $P'$ on the west side across from me ( $\overline{P_0P'}=m$ ).

I walked north to the next lamppost $P_1$ ,and discovered that the distance $\overline{P_1P'}$ is an integer.

I keep walking north to one of the lamppost $P_x$ ,and discovered that the distance $\overline{P_xP'}$ is an integer,too.

What is the minimum width $m$ of the road(in meters)?

Note that I keep walking on the east side of the road.

Picture Source:From Jeremy Galvagni.

Try my set here

The answer is 12.

2 solutions

David Vreken
Aug 7, 2018

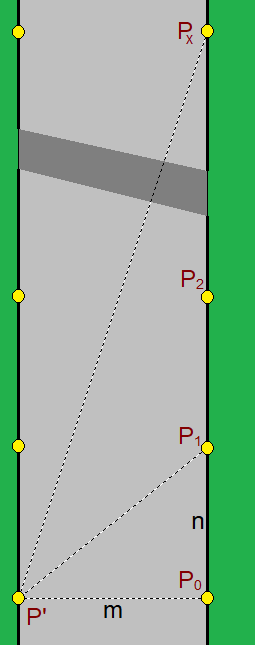
Both $\triangle P'P_0P_1$ and $\triangle P'P_0P_x$ are right triangles with integer sides, so we need two sets of Pythagorean triples with the same leg $P_0P' = m$ and the other leg ( $P_0P_x$ ) that is a multiple of the first ( $P_0P_1 = n$ ).

The Pythagorean triples $(5, 12, 13)$ and $(12, 35, 37)$ meet the criteria with $m = 12$ , $n = 5$ , and $P_0P_x = 5 \cdot 7 = 35$ .

This is also the smallest possible value for $m$ by looking at a complete list of Pythagorean triples found here . Pythagorean triples with legs of $1$ and $2$ do not exist, and the Pythagorean triples with legs $3$ , $4$ , $5$ , $6$ , $7$ , $10$ , and $11$ only appear once. A leg of $8$ appears twice ( $(6, 8, 10)$ and $(8, 15, 17)$ ) but $15$ is not a multiple of $6$ , and a leg of $9$ appears twice ( $(9, 12, 15)$ and $(9, 40, 41)$ ) but $40$ is not a multiple of $12$ . By elimination this means that the smallest possible value of $m$ is $m = \boxed{12}$ .

Why not m=0 a solution? It's not told in the problem that m>0

A Former Brilliant Member - 2 years, 3 months ago

When describing a measurement of a physical object (such as the width of the road), it's typically assumed to be positive.

David Vreken - 2 years, 3 months ago

Jeremy Galvagni
Aug 8, 2018

I can't do better than @David Vreken's solution, and I'm not a moderator, but here's a nice picture you can copy and insert in your problem.

Thank you very much!!

X X - 2 years, 10 months ago

No troubles. Now if you edit the problem you can change the link slightly. Change the word center to either left or right and it will shift the picture and place the text to the side.

Jeremy Galvagni - 2 years, 10 months ago

Thanks for the imformation!I didn't know this before.

X X - 2 years, 10 months ago

Minimum Road Width

The answer is 12.

2 solutions

0 pending reports