Minimum sum of areas
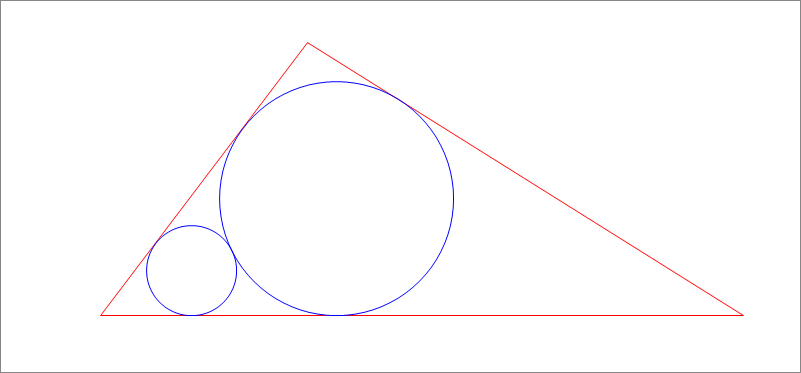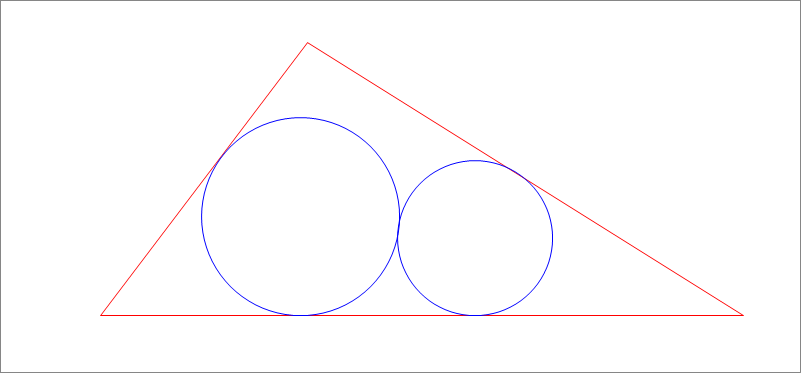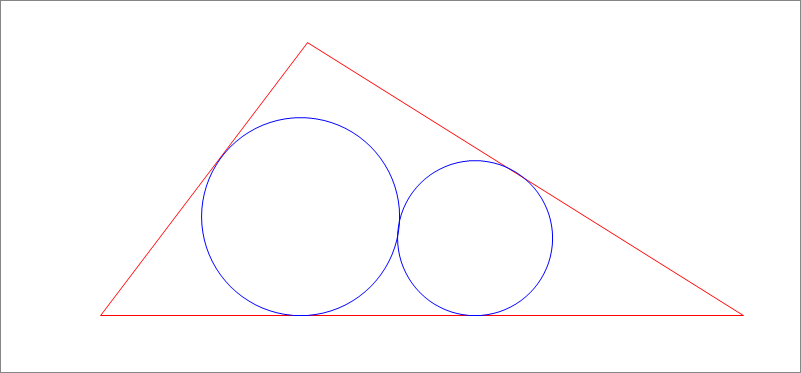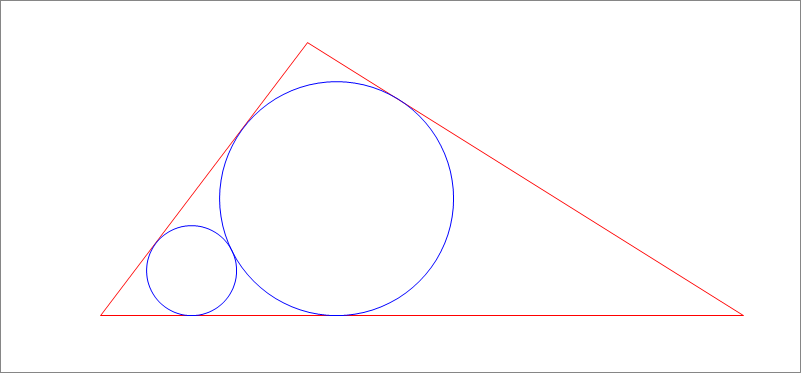
In , . Two tangent circles are to be inscribed in the triangle as shown in the figure above. They are both tangent to , with the left one tangent to , while the right one is tangent to . If is the minimum sum of the areas of the two circles , enter
The answer is 2446086.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the center and radius of the left circle be O and r and those of the right circle be P and R . O D and P E be perpendicular to B C , and O F perpendicular to P E . Then the length of B C is given by:
B D + D E + E C O D ⋅ cot 2 B + O F + P E ⋅ cot 2 C O D ⋅ cot 2 B + O P 2 − P F 2 + P E ⋅ cot 2 C r cot 2 B + ( R + r ) 2 − ( R − r ) 2 + R cot 2 C R cot 2 C + 2 r R + r cot 2 B − 1 5 = B C = B C = B C = 1 5 = 0
The above equation is a quadratic equation for R , and we can express R in terms of r as follows.
R = 2 cot 2 C 4 r − 4 cot 2 C ( r cot 2 B − 1 5 ) − 2 r
Given the side lengths of △ A B C , we can find the measures of angles A , B , and C . Therefore we can compute R for a particular r and hence S ( r ) = π ( r 2 + R 2 ) , and find S min = min ( S ( r ) ) . I used an Excel spreadsheet to compute R and S ( r ) and found S min ≈ 2 4 . 4 6 0 8 6 3 4 4 , when r ≈ 1 . 6 5 0 8 9 0 9 1 7 . Therefore 1 0 5 S min = 2 4 4 6 0 8 6 .