Grown pentagram

It is given that $f(z) = z^4+z^3+z^2+z+1 = 0$ .

Multiplying it with $z$ : $\Rightarrow z^5+ z^4+z^3+z^2+z= 0$

Adding $1$ on both sides: $\Rightarrow z^5+ z^4+z^3+z^2+z + 1= 1$

$\Rightarrow z^5 = 1 = \cos{2k\pi}+i\sin{2k \pi} = e^{2\pi i}$ , where $i = \sqrt{-1}$ and $k = 1,2,3,4$ . Therefore,

$z = e^{i\frac{2k\pi}{5}} = \begin{cases} \cos{\frac{2\pi}{5}}+i\sin{\frac{2\pi}{5}} \\ \cos{\frac{4\pi}{5}}+i\sin{\frac{4\pi}{5}} \\ \cos{\frac{6\pi}{5}}+i\sin{\frac{6\pi}{5}} = \cos{\frac{4\pi}{5}}-i\sin{\frac{4\pi}{5}} \\ \cos{\frac{8\pi}{5}}+i\sin{\frac{8\pi}{5}} = \cos{\frac{2\pi}{5}}-i\sin{\frac{2\pi}{5}} \end{cases}$

Possible values of $z_1+z_2$ are as follows:

$z_1+z_2=\begin{cases} \cos{\frac{2\pi}{5}}+\cos{\frac{4\pi}{5}} + i( \sin{\frac{2\pi}{5}}+ \sin{\frac{4\pi}{5}}) \\ \cos{\frac{2\pi}{5}}+\cos{\frac{4\pi}{5}} + i( \sin{\frac{2\pi}{5}}- \sin{\frac{4\pi}{5}} ) \\ 2\cos{\frac{2\pi}{5}} \\ 2\cos{\frac{4\pi}{5}} \\ \cos{\frac{2\pi}{5}}+\cos{\frac{4\pi}{5}} - i( \sin{\frac{2\pi}{5}}- \sin{\frac{4\pi}{5}} ) \\ \cos{\frac{2\pi}{5}}+\cos{\frac{4\pi}{5}} - i( \sin{\frac{2\pi}{5}}+\sin{\frac{4\pi}{5}} ) \end{cases}$

Possible values of $|z_1+z_2|$ are as follows:

$|z_1+z_2|=\begin{cases} |2\cos{\frac{2\pi}{5}}| = 0.618033989 \\ |2\cos{\frac{4\pi}{5}}| = 1.618033989 \end{cases}$

Therefore, $\min {\lfloor |z_1+z_2| \rfloor } = \lfloor 0.618033989 \rfloor = \boxed{0}$

Those are the complex fifth roots of unity, whixh lie on a regular pentagon on unit circle. So, 0<| $z_1 + z_2$ |<1 and floor value is 0.

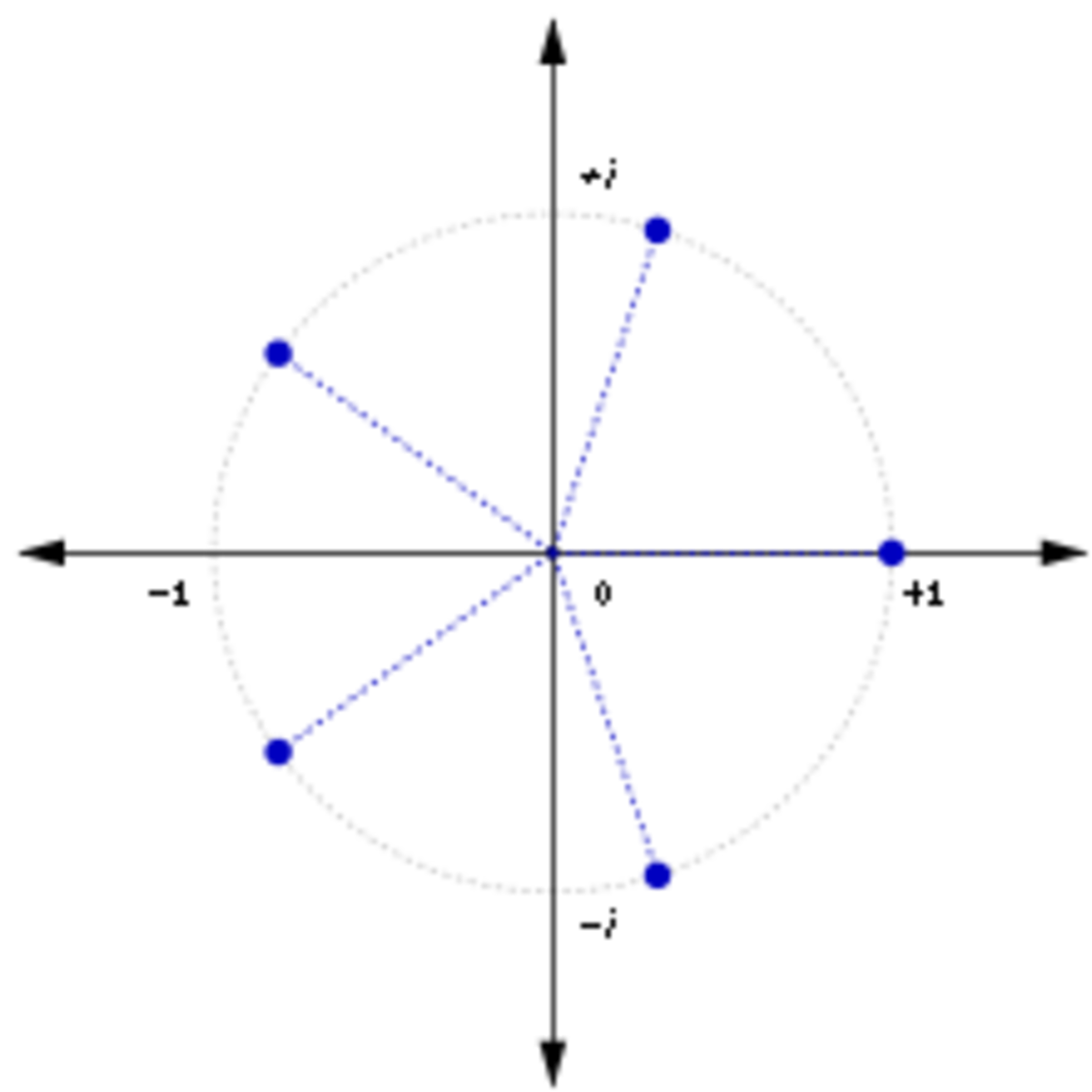This could also be done easily if we graph the fifth roots of unity, where we have a pentagon. Then, we have to analyze the four angles(72, 144, 216, 288.) To have the minimum, we need to cancel the sines or cosines at least, so when we graph the pentagon in the complex plane, we find that 72 and 288, or 144 and 216 have their sines canceled out. Now, we resort to find the min values of the sum of the real values(the cosines). cos72 + cos288 have a lower cosine than cos(144 ) + cos216(this can be easily seen when a complex pentagon is accurately graphed. Thus, the magnitude is little greater than 0.5 and less than 1, so the floor function is 0.