Minimum value of equations #4
Non-negative real numbers x , y , and z are such that x 2 + y 2 + z 2 ≤ 3 y . Find the minimum value of the expression below:
( x + 1 ) 2 1 + ( y + 2 ) 2 4 + ( z + 3 ) 2 8
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Care to elaborate? How did you arrive at this solution? Have you tested all uncountably many values of x , y , z ?
It is not necessary to test all uncountably many values of x , \y) and z . This is a 2-dimensional minimization problem solvable with calculus. You are looking for places with the derivative in each direction being 0 . The cross-sections of the function to be minimized are nested hyperbolae with the higher valued surfaces closer to the center of the overall figure. To minimize the function, one needs to examine such surfaces that pass through the furthermost point of the region of interest which is a ball. One is only concerned with the boundary of the search as the sign of the derivative never changes over the region of interest and therefore the extrema are on the surface of the region of interest. The fact that surfaces are hyperboloids can be read from the structure of the function to be minimized. The fact that the region of interest is a ball can be read from the structure of expression describing the region of interest.
Here is a plot of the problem. The small ball is the region of interest. The surface where the function equals 1 (the minimum value) is garayish-blue surface in the nested surfaces.
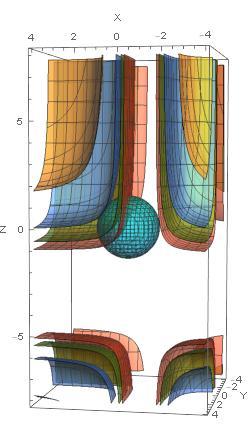
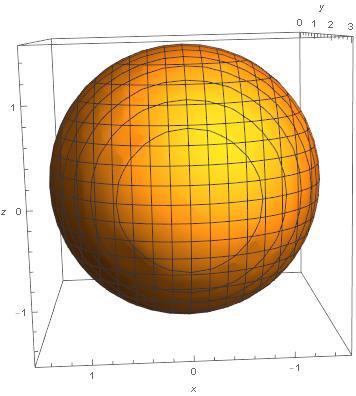
This is the region of interest, a ball.
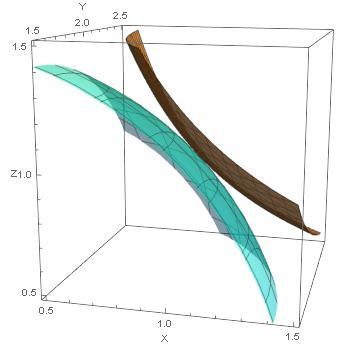
Here is a region around the point of contact.
Log in to reply
Thank you for your explanation.
Further questions:
1) What app did you use to generate these graphs? Wolfram Mathematica again?
2) What if there are more than 3 variables here? We can't possibly produce the graphs anymore since we are only able to perceive 3-dimensional figures. Will plain calculus (and all the derivative tests like Hessian matrix) still do the trick?
1) Yes
2) Yes
The first illustration effectively is a four dimensional situation projected to a two dimensional surface as the colors provide a fourth dimensional.
Minimize [ { ( x + 1 ) 2 1 + ( y + 2 ) 2 4 + ( z + 3 ) 2 8 , x 2 + y 2 + z 2 ≤ 3 y } , { x , y , z } , R ] ⇒ { 1 , { x → 1 , y → 2 , z → 1 } } .