Minimum value#3
In a right-angled triangle
(
),
are three angle bisectors.
is the intersection point of
and
.
lie on
respectively such that
.
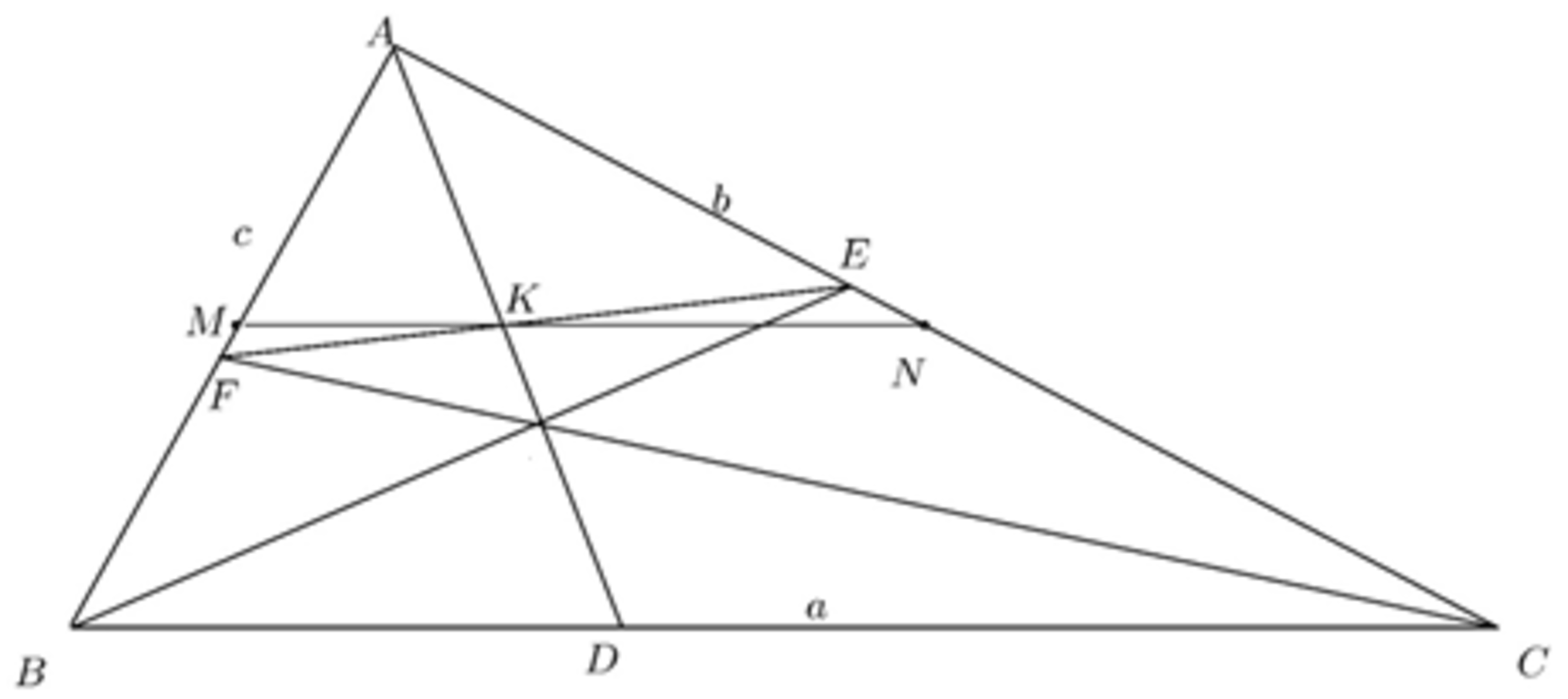
Find the minimum value of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let B C = a , C A = b , A B = c , then we have a , b , c > 0 , a 2 = b 2 + c 2 ≥ 2 ( b + c ) 2 (by applying Pythagorean theorem and AM-GM inequality).
⟹ a b + c ≤ 2 ( 1 ) .
By applying Angle bisector theorem,
B F A F = a b ⟹ A B A F = a + b b = c A F ⟹ A F = a + b b c .
Similarly, A E = a + c b c .
Also, we notice that
A r e a A B C = A r e a A B D + A r e a A D C ⟹ b c = A D ( c sin A B D + b sin C A D ) = A D × 2 1 ( b + c ) ⟹ A D = b + c 2 b c .
By similarly, A K = A E + A F 2 A E . A F = 2 a + b + c 2 b c .
So,
A D A K = 2 a + b + c b + c ⟹ a M N = 2 a + b + c b + c ⟹ M N = 2 a + b + c a ( b + c ) = 2 + a b + c b + c ≥ 2 + 2 b + c (from ( 1 ) )
⟹ M N ≥ 2 2 − 2 ( A B + A C ) ⟹ A B + A C M N ≥ 2 2 − 2 = 1 − 2 2
Hence, ( A B + A C M N ) m i n = 1 − 2 2 when b = c = 2 a 2