Minimum Velocity Required to move in a circle!
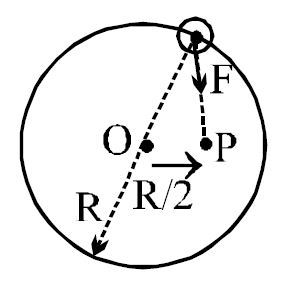 A small bead of mass
m
can move on a smooth circular wire (radius
R
) under the action of a force
F
=
r
2
K
m
only directed (denote constant
r
as the position of bead from
P
and
K
) towards a point
P
with in the circle at a distance
2
R
from the center.
A small bead of mass
m
can move on a smooth circular wire (radius
R
) under the action of a force
F
=
r
2
K
m
only directed (denote constant
r
as the position of bead from
P
and
K
) towards a point
P
with in the circle at a distance
2
R
from the center.
What should be the minimum velocity of bead at the point of the wire nearest the center of force ( P ) so that bead will complete the circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Angular momentum won't conserve due to torque by normal reaction..
Plz post a solution, i just got lucky
Clearly angle OKP =30 degrees Now find out the component of the force F along KO....equate this force with centripetal force...don't forget to find out "r" in terms of "R" and substitute it
Log in to reply
Do correct me if I were wrong.
F cos 3 0 o = m R v 2 and r = 2 3 R
But this doesn't gives the answer.
simply get the difference b/w minimum and maximum potential energy (since it follows inverse square law u are much aware abt that) and equate it to minimum ke req.
Actually, the velocity is never just a value. That is the speed .
So, theoretically, the answer is None of these .
See this problem for disambiguation.
The answer is wrong upon conservation of angular momentum at point from where force acts you get the answer