Minimum Vertex Cover
Computer Science
Level
1
What is the least number of nodes you can have to make a minimum vertex cover of this graph?
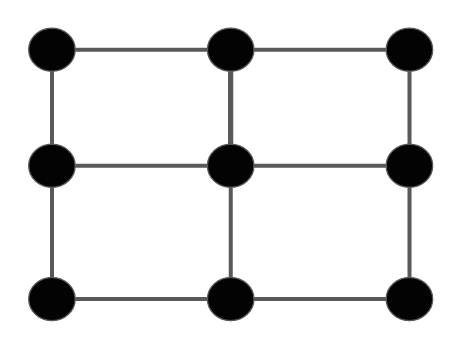
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The answer is 4.
One way to think about the problem is to color all of the nodes red, this is certainly a vertex cover since all of the nodes are in the cover and all of the edges must touch one of those nodes. Start removing nodes by coloring them black. If coloring a node black causes any of the edges to become disconnected from the cover, you have to turn one of the nodes touching the soon-to-be disconnected edge red.
Any set of red vertices that keeps all the edges touching a red vertex is a vertex cover, but the minimum vertex cover is the lowest number of nodes needed to still have a cover. This means that if we disconnect any node in a minimum vertex cover, the resulting set of vertices is no longer a cover.