Mirror Mirror Hologram

Calculus Level 5

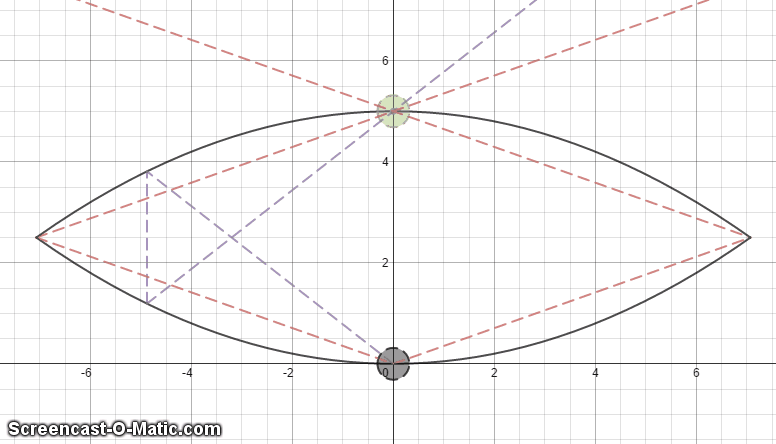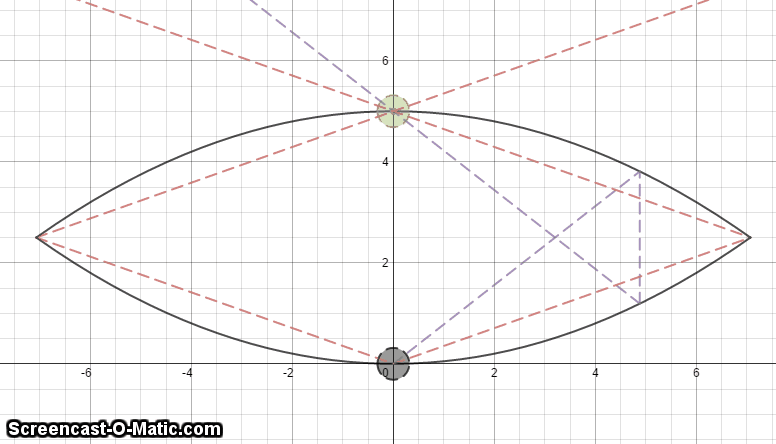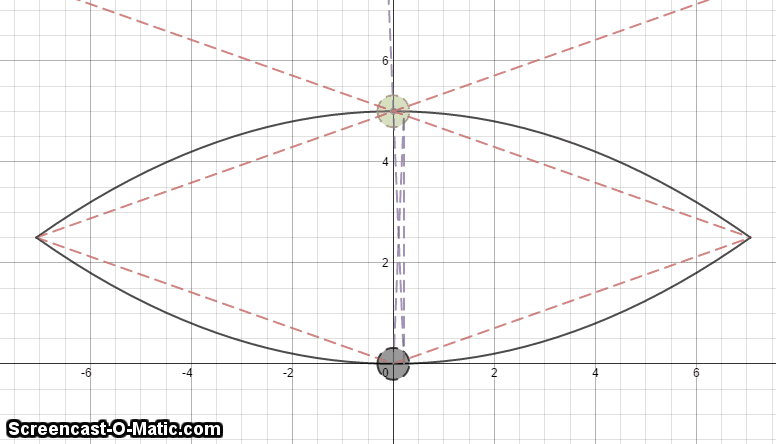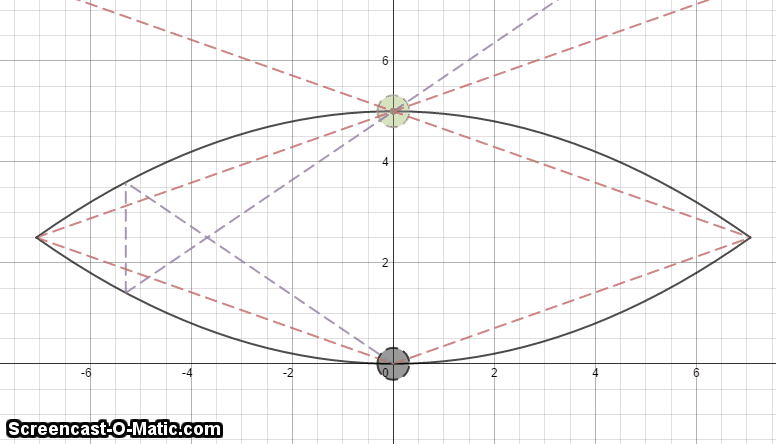
The image above is of a hologram.

In the GIF, the Black ball is the real object and the Green ball is the virtual image produced.

The Black lines represents the hologram itself and is coated on the inside with a Chrome layer, such that inside the hologram acts like a mirror. (As shown in the GIF)

The Red lines represents the maximum the light can go.

The Red lines indicate that there are some parts of the object where the virtual image does not show:

So now, here's the question:

Dr Boh wants to get a hologram that has a height of $5$ , and also wants to find the volume of the hologram that he would be getting. Given that the volume of that hologram is $A$ , find $\left\lfloor 100A \right\rfloor$

Details and Assumptions :

The height of the holograph is defined as:
You might want to take a look at Brusspup's video first to get an idea of how a hologram works

The answer is 39269.

1 solution

Raghav Vaidyanathan
Apr 3, 2015

@Julian Poon , I must say, your GIFs make your problems infinitely more interesting and easier!

Looking at the animated GIF, it is easy to see that the all the rays from the object get reflected vertically downwards by the top surface and further, all the vertically reflected rays get reflected by the bottom surface to converge at the top of the construction.

The top and bottom are obviously symmetrical. This leads to a simple question: Mirror, Mirror on the wall, which shape converges all them parallel rays?

And the answer comes, clear and sure: Snow White! Oops. I mean: Parabola!

The two surfaces are paraboloids which are put upside down on each other such that the vertex of one coincides with the focus of the other. Take a moment to convince yourself of this.

Now, the defining factor of each paraboloid has been given. That is: the distance between the focus and the vertex is given as $5$ . Hence, we can write the equation of each of the paraboloid halves as: $y^2+z^2=4ax$ between $0 \text{and} 5/2$ . This is basically just a 2-D parabola rotated about x-axis. Now, at $x=5/2$ , the radius of the cross section of the parabola is $\sqrt{50}$ .

Now comes the fun part: We only have to calculate the volume of one half of the hologram and then double it. Observe that the cylinder which exactly encloses the given paraboloid has height $5/2$ and radius $\sqrt{50}$ . The volume of a paraboloid is half of the volume of this cylinder*. Hence, the requred volume is simply the volume of the cylinder.

$A=\pi r^2 h= \pi 25*5=392.699$

$\left\lfloor 100A \right\rfloor =\boxed{39269}$

*The derivation of this result is interesting and useful, and so, it is left as an exercise to the reader

Thanks! And that's a great geometrical approach! I wasn't aware that the volume of a paraboloid is half the volume of the cylinder.

Julian Poon - 6 years, 2 months ago

Thank you! Actually, I came across this result while doing a problem on the parabolic surface formed by a rotating beaker of liquid. This result is similar to the others like:

$\text{volume of pyramid}=1/3(\text{volume of corresponding prism})$ .

Raghav Vaidyanathan - 6 years, 2 months ago

Mirror Mirror Hologram

The answer is 39269.

1 solution

0 pending reports