Mirroring the Slopes (Count 'em All 19!)
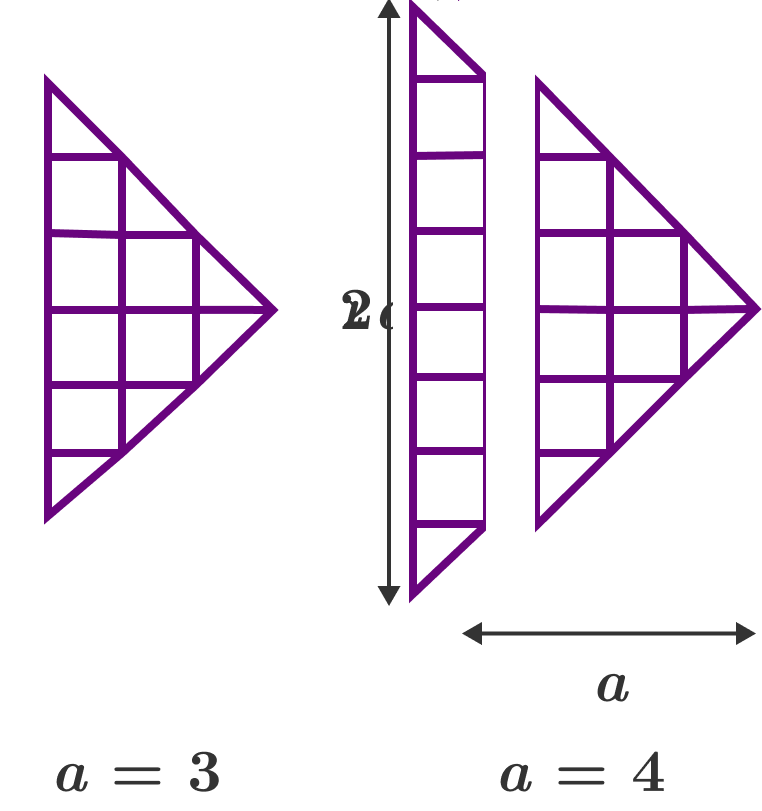
A right arrow grid with base length 2 a is defined to be an a × a grid cut into 2 halves diagonally, and then put together as illustrated.
What is the total number of quadrilaterals in a right arrow grid with a = 3 0 ?
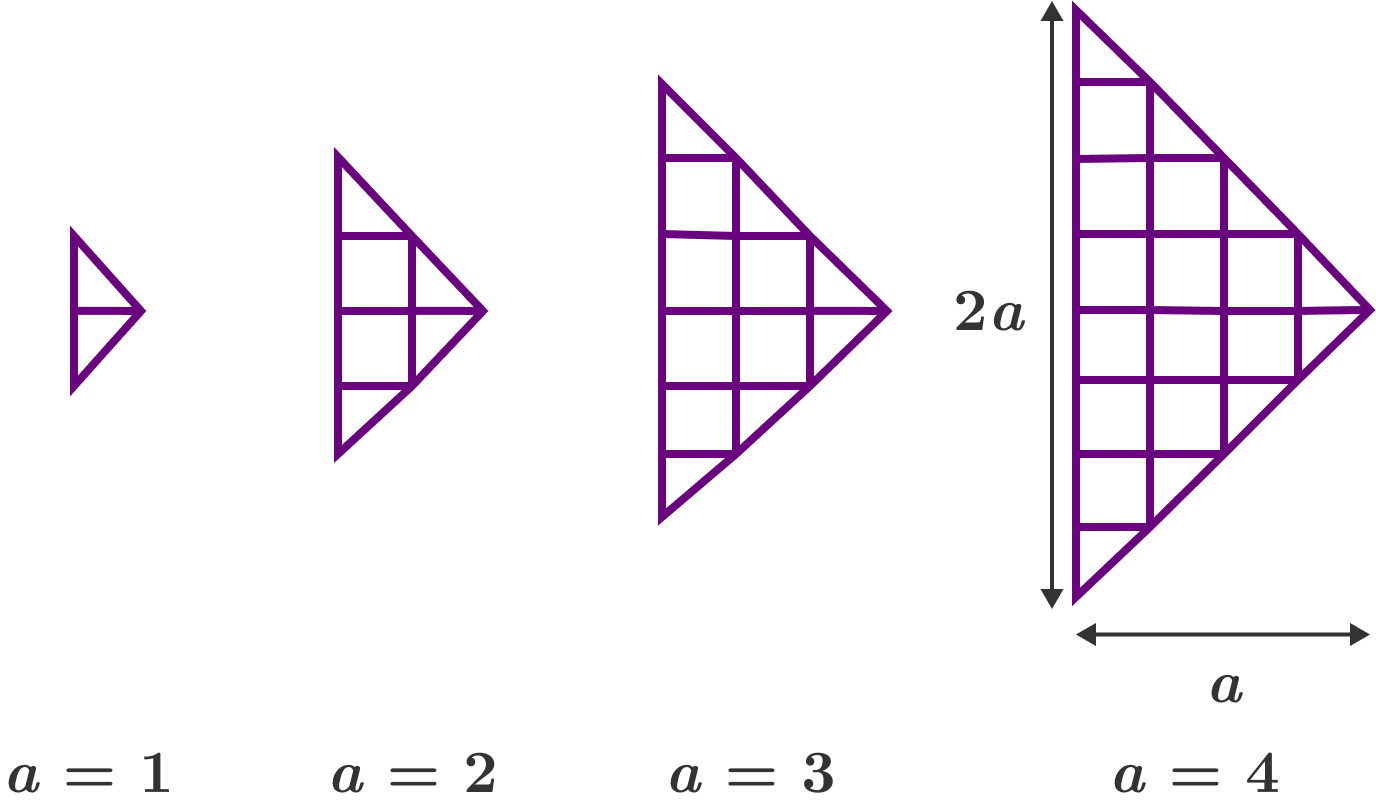
The answer is 167620.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions

The right arrow grid is made from 2 individual slope grids. The number of quadrilaterals in each of the 2 slope grids is 2 4 a ( a − 1 ) ( a + 1 ) ( a + 1 0 )
Here's a quick sketch of a proof for this formula, you can see more details of this proof in my solution to Count 'em Slopes (Count 'em All 17!) , if you've already seen it, you may safely skip this part. :D
Proof:
Before we dive into slope grids, I shall prove first that the number of quadrilaterals in an a × a staircase grid is 2 4 a ( a + 1 ) ( a + 2 ) ( a + 3 )
Suppose the number of quadrilaterals in an a × a staircase grid is Q a , we will try to find Q a + 1 .
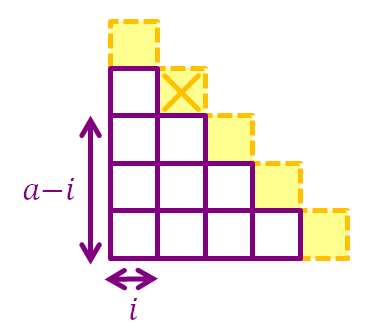
To increase a by 1, we simply add a + 1 squares to the hypotenuse (the yellow squares), the newly formed quadrilaterals must contain one of the yellow squares as its top-right corner square. If a quadrilateral's top-right corner square lies on a yellow square that is i units away from the left boundary, then it must be a − i units away from the bottom boundary, and the number of possible locations for its bottom-left corner square is ( i + 1 ) ( a − i + 1 ) .
Therefore, Q a + 1 = Q a + i = 0 ∑ a ( i + 1 ) ( a − i + 1 ) = Q a + 6 a 3 + 6 a 2 + 1 1 a + 6 .
Solving this recurrence relation with the initial condition Q 1 = 1 , we get that Q a = 2 4 a ( a + 1 ) ( a + 2 ) ( a + 3 ) . □
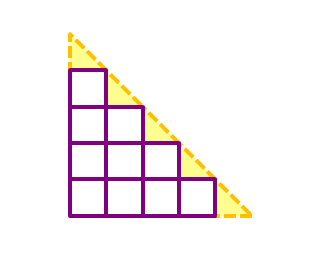
Back to slope grids, we observe that an a × a slope grid consists of an ( a − 1 ) × ( a − 1 ) staircase grid with a triangles patched along its hypotenuse. The number of quadrilaterals in the ( a − 1 ) × ( a − 1 ) staircase grid is 2 4 a ( a − 1 ) ( a + 1 ) ( a + 2 ) .
We now just need to count the remaining trapeziums.
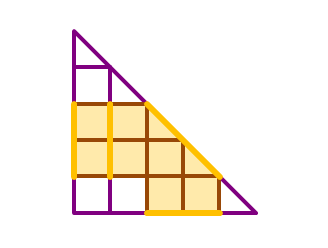
To construct a trapezium, we choose a certain length of the slanted edge of the slope grid. The number of ways to choose a slanted edge of length i ( i ∈ Z + , i ⩽ a ) is a − i + 1 . Then, we need either a matching left edge for the trapezium or a matching bottom edge for the trapezium. The total number of ways to do so with the chosen slanted edge of length i is a − i . Therefore, the total number of trapeziums is i = 1 ∑ a ( a − i ) ( a − i + 1 ) = 6 a ( a − 1 ) ( 2 a − 1 ) + 2 a ( a − 1 ) .
Therefore, the number of quadrilaterals in an a × a slope grid is 2 4 a ( a − 1 ) ( a + 1 ) ( a + 2 ) + 6 a ( a − 1 ) ( 2 a − 1 ) + 2 a ( a − 1 ) = 2 4 a ( a − 1 ) ( a + 1 ) ( a + 1 0 ) . □
The total number of quadrilaterals in the two slope grids is 2 × 2 4 a ( a − 1 ) ( a + 1 ) ( a + 1 0 ) = 1 2 a ( a − 1 ) ( a + 1 ) ( a + 1 0 ) .
It now remains to count the number of "crossover" quadrilaterals (quadrilaterals that cross the common boundary of both slope grids). We'll construct the crossover quadrilaterals by picking one square or triangle from the top slope grid as its top-right corner square or triangle, and one square or triangle from the bottom slope grid as its bottom-left corner square or triangle (if any of its corners are triangles, the resulting quadrilateral would be a trapezium).
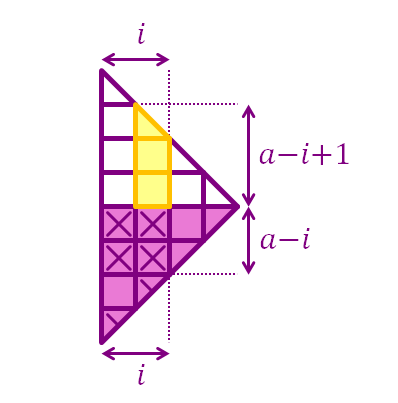
Consider picking one square or triangle in the i -th column ( i ∈ Z + ) from the left of the top slope grid where 1 ⩽ i ⩽ a − 1 . The height of that column is a − i + 1 .
Now we pick its corresponding bottom-left corner square or triangle from the bottom slope grid so that it forms a valid quadrilateral. Valid bottom-left corners consist of the corresponding i × ( a − i ) squares in the bottom slope grid, plus the additional i triangles below the i × ( a − i ) region, making a total of i ( a − i + 1 ) valid bottom-left corners.
Thus, the total number of quadrilaterals that can be formed with its top-right corner in the i -th column where 1 ⩽ i ⩽ a − 1 is i ( a − i + 1 ) 2 ,

For i = a , things are a little bit different. If we choose the only triangle in this column as the quadrilateral's top right corner, its valid bottom-left corners consist of the internal squares of the bottom slope grid and we get napkin-like trapeziums. In this case, for i = a , the number of valid bottom-left corners is 2 a ( a − 1 ) . Since the right arrow grid is symmetric, we can do the same thing with the sides switched (top slope grid and bottom slope grid swapped). We get the same set of napkin trapeziums but mirrored. The total number of napkin trapeziums is 2 × 2 a ( a − 1 ) = a ( a − 1 ) .
Thus the total number of crossover quadrilaterals is [ i = 1 ∑ a − 1 i ( a − i + 1 ) 2 ] + a ( a − 1 ) = { i = 1 ∑ a i [ ( a + 1 ) 2 − 2 ( a + 1 ) i + i 2 ] } + a ( a − 1 ) = { i = 1 ∑ a − 1 [ ( a + 1 ) 2 i − 2 ( a + 1 ) i 2 + i 3 ] } + a ( a − 1 ) = 2 a ( a − 1 ) ( a + 1 ) 2 − 3 a ( a − 1 ) ( a + 1 ) ( 2 a − 1 ) + [ 2 a ( a − 1 ) ] 2 + a ( a − 1 ) = a ( a − 1 ) [ 2 ( a + 1 ) 2 − 3 ( a + 1 ) ( 2 a − 1 ) + 4 a ( a − 1 ) + 1 ] = 1 2 a ( a − 1 ) [ 6 a 2 + 1 2 a + 6 − 4 ( 2 a 2 + a − 1 ) + 3 a 2 − 3 a + 1 2 ] = 1 2 a ( a − 1 ) ( a 2 + 5 a + 2 2 )
Therefore, the total number of quadrilaterals in an a -tiered right arrow grid is 1 2 a ( a − 1 ) ( a + 1 ) ( a + 1 0 ) + 1 2 a ( a − 1 ) ( a 2 + 5 a + 2 2 ) = 1 2 a ( a − 1 ) ( 2 a 2 + 1 6 a + 3 2 ) = 6 a ( a − 1 ) ( a 2 + 8 a + 1 6 ) = 6 a ( a − 1 ) ( a + 4 ) 2
Now, substituting a = 3 0 , we would get the answer 1 6 7 6 2 0 .
Here is my solution.
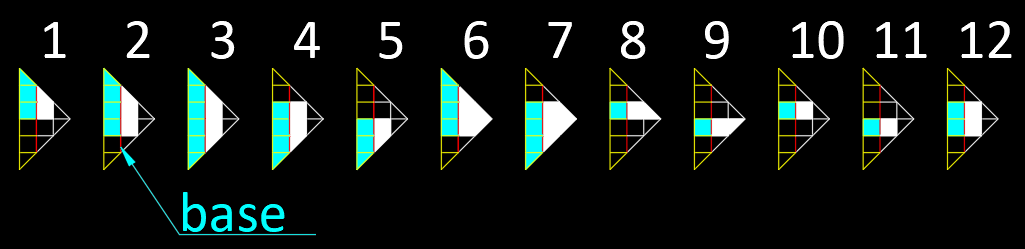
First, I draw all 12 solutions for
a
=
2

Second, I tried to find an incremental path for a = 3
 Eventually, it came out that all
a
=
2
solutions
touching the base
(which are all of them but that will not be the case for
a
>
2
), can be stretched to
a
=
3
solution. (Let's call this set of solutions
A
1
)
Eventually, it came out that all
a
=
2
solutions
touching the base
(which are all of them but that will not be the case for
a
>
2
), can be stretched to
a
=
3
solution. (Let's call this set of solutions
A
1
)
A 1 = n u m b e r o f s o l u t i o n s t o u c h i n g t h e b a s e
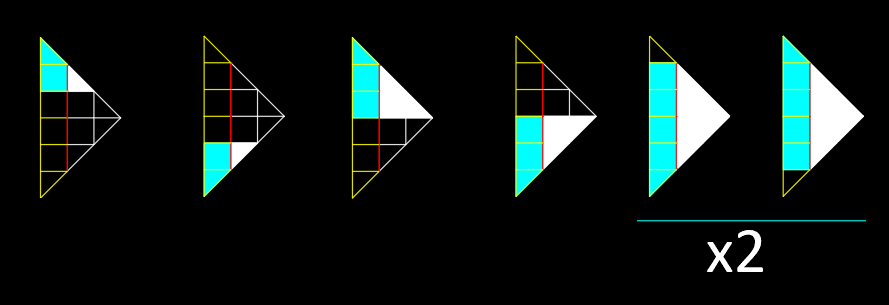 We can also stretch triangles (which are not
a
=
2
solutions) to get another set of
a
=
3
solutions. (We will call this set
B
)
We can also stretch triangles (which are not
a
=
2
solutions) to get another set of
a
=
3
solutions. (We will call this set
B
)
B = 2 ( a − 1 ) + 2 = 2 a
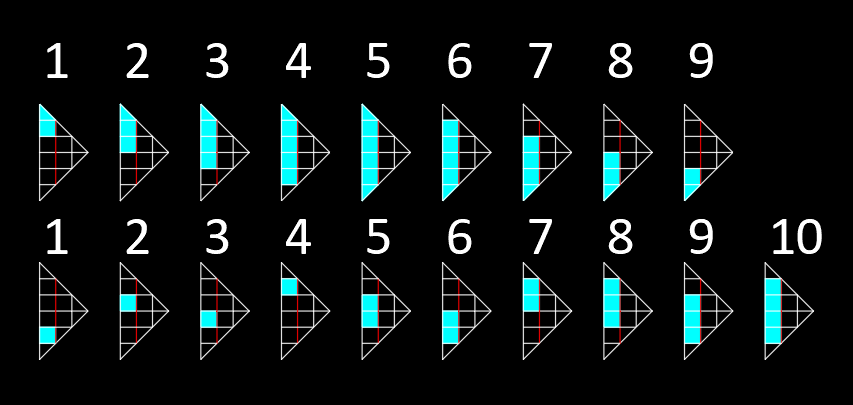
And rest of the a = 3 solutions lie on the left side of the red line (Call this set C )
C = 2 ( 2 a − 2 ) ( 2 a − 1 ) + 2 ( 2 a − 2 ) + 1 = 2 ( 2 a − 2 ) ( 2 a + 3 ) + 1
Finally, the update equations are as follows:
A 1 = C + B + A 1 ( a − 1 )
T o t a l = T o t a l ( a − 1 ) + A 1
| a | T o t a l ( a − 1 ) | C | A 1 ( a − 1 ) | B | A 1 | T o t a l |
| 2 | 12 | 12 | ||||
| 3 | 12 | 19 | 12 | 6 | 37 | 49 |
| 4 | 49 | 34 | 37 | 8 | 79 | 128 |
| 5 | 128 | 53 | 79 | 10 | 142 | 270 |
| 6 | 270 | 76 | 142 | 12 | 230 | 500 |
| 7 | 500 | 103 | 230 | 14 | 347 | 847 |
| 8 | 847 | 134 | 347 | 16 | 497 | 1344 |
| 9 | 1344 | 169 | 497 | 18 | 684 | 2028 |
| 10 | 2028 | 208 | 684 | 20 | 912 | 2940 |
| 11 | 2940 | 251 | 912 | 22 | 1185 | 4125 |
| 12 | 4125 | 298 | 1185 | 24 | 1507 | 5632 |
| 13 | 5632 | 349 | 1507 | 26 | 1882 | 7514 |
| 14 | 7514 | 404 | 1882 | 28 | 2314 | 9828 |
| 15 | 9828 | 463 | 2314 | 30 | 2807 | 12635 |
| 16 | 12635 | 526 | 2807 | 32 | 3365 | 16000 |
| 17 | 16000 | 593 | 3365 | 34 | |3992 | 19992 |
| 18 | 19992 | 664 | 3992 | 36 | 4692 | 24684 |
| 19 | 24684 | 739 | 4692 | 38 | 5469 | 30153 |
| 20 | 30153 | 818 | 5469 | 40 | 6327 | 36480 |
| 21 | 36480 | 901 | 6327 | 42 | 7270 | 43750 |
| 22 | 43750 | 988 | 7270 | 44 | 8302 | 52052 |
| 23 | 52052 | 1079 | 8302 | 46 | 9427 | 61479 |
| 24 | 61479 | 1174 | 9427 | 48 | 10649 | 72128 |
| 25 | 72128 | 1273 | 10649 | 50 | 11972 | 84100 |
| 26 | 84100 | 1376 | 11972 | 52 | 13400 | 97500 |
| 27 | 97500 | 1483 | 13400 | 54 | 14937 | 112437 |
| 28 | 112437 | 1594 | 14937 | 56 | 16587 | 129024 |
| 29 | 129024 | 1709 | 16587 | 58 | 18354 | 147378 |
| 30 | 147378 | 1828 | 18354 | 60 | 20242 | 167620 |
This is how I calculated it: n = 1 ∑ 2 9 ( n ( 3 0 − n ) ( 6 1 − 2 n ) + 2 n ( 6 0 − 2 n ) + 2 n ( 3 0 − n ) + n + 2 n ) = 1 6 7 6 2 0
I tried to do something like this but got it wrong. I always like the simplest most elegant solution
After complex operations
F(a)=2F(a-1)-F(a-2)+4(a-1)+a(2a-1)+2
First, we classify the quadrilaterals into five cases. The formula for the number of each is given
Vertical symmetric trapezoids
F 1 ( n ) = 2 1 ( n − 1 ) n
Vertical non-symmetric trapezoids
F 2 ( n ) = 3 2 ( n − 1 ) n ( n + 1 )
Horizontal non-symmetric trapezoids
F 3 ( n ) = 3 1 ( n − 1 ) n ( n + 1 )
Irregular quadrilaterals
F 4 ( n ) = ( n − 1 ) n
Rectangles
F 5 ( n ) = 6 1 ( n − 1 ) n ( n + 1 ) 2
When added all together, the final formula works out to
F ( n ) = 6 1 ( n − 1 ) n ( n + 4 ) 2
So that the the first few values are 0 , 1 2 , 4 9 , 1 2 8 , and
F ( 3 0 ) = 1 6 7 6 2 0