Mirroring the Staircases (Count 'em All 18!)
A pixelated right arrow grid is a grid of squares that is made by mirroring a staircase grid along its base. For example, the figure below shows 4 pixelated right arrow grids with tiers 1, 2, 3 and 4 respectively.
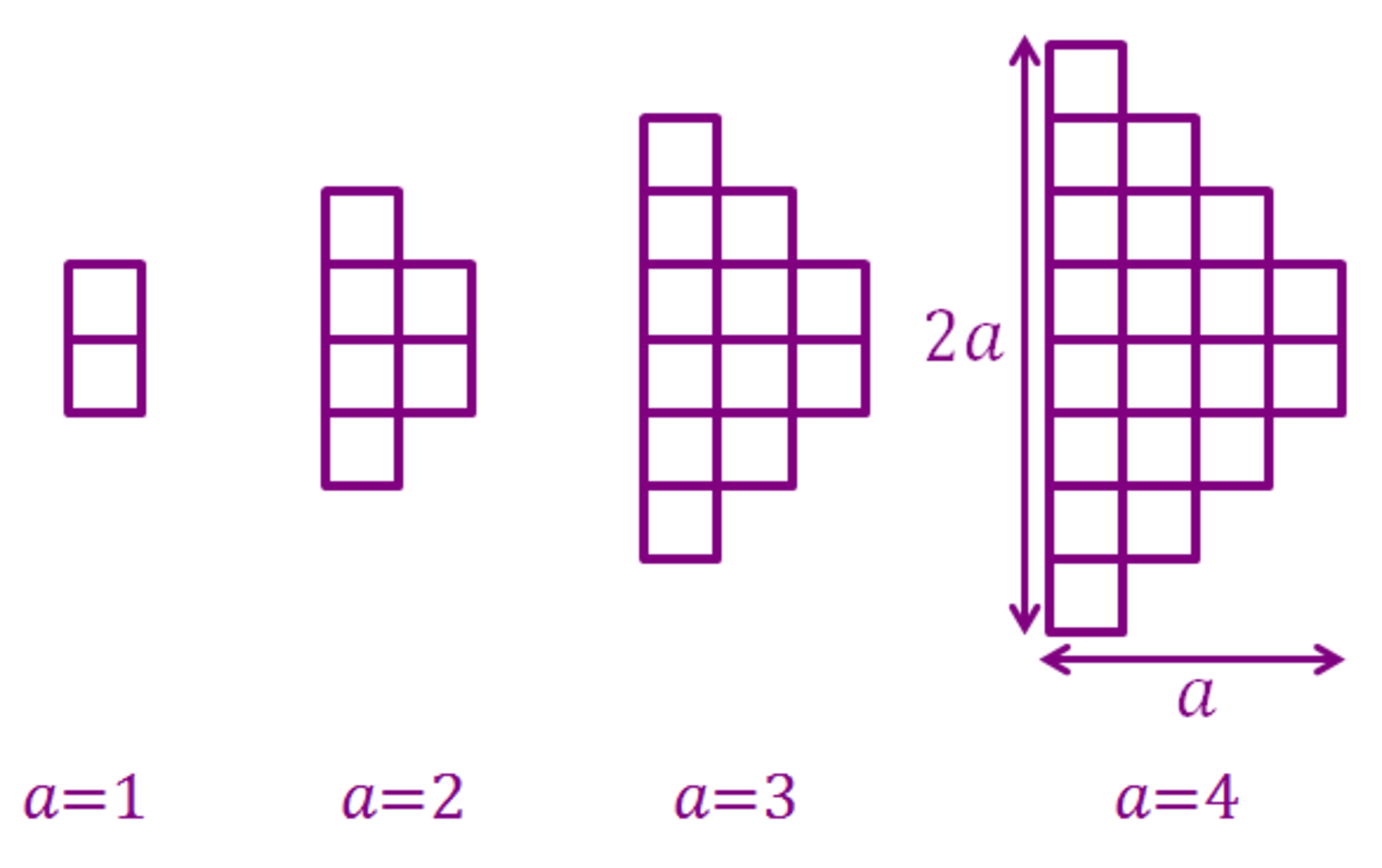
Count the total number of quadrilaterals in a 30-tiered pixelated right arrow grid (that is, when ).
Clarification:
- A quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 158720.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The pixelated right arrow grid is made from 2 individual staircase grids. The number of quadrilaterals in each of the 2 staircase grids is 2 4 a ( a + 1 ) ( a + 2 ) ( a + 3 )
Here's a quick sketch of a proof for this formula, you can see the full details of this proof in my solution to Count 'em Staircases (Count 'em All 16!) , if you've already seen it, you may safely skip this part. :D
Hence, the total number of quadrilaterals in the two staircase grids is 2 × 2 4 a ( a + 1 ) ( a + 2 ) ( a + 3 ) = 1 2 a ( a + 1 ) ( a + 2 ) ( a + 3 ) .
It now remains to count the number of "crossover" quadrilaterals (quadrilaterals that cross the common boundary of both staircase grids). We'll construct the crossover quadrilaterals by picking one square from the top staircase grid as its top-right corner square, and one square from the bottom staircase grid as its bottom-left corner square.
Consider picking one square in the i -th column ( i ∈ Z + , 1 ⩽ i ⩽ a ) from the left of the top staircase grid. The height of that column is a − i + 1 .
Now we pick its corresponding bottom-left corner square from the bottom staircase grid so that it forms a valid quadrilateral, all valid bottom-left corner squares for the chosen top-right corner square are indicated by an 'X' as shown in the figure above, the size of this 'X' region is i × ( a − i + 1 ) .
Thus, the total number of quadrilaterals that can be formed with its top-right corner square in the i -th column is i ( a − i + 1 ) 2 , and thus the total number of crossover quadrilaterals is i = 1 ∑ a i ( a − i + 1 ) 2 = i = 1 ∑ a i [ ( a + 1 ) 2 − 2 ( a + 1 ) i + i 2 ] = i = 1 ∑ a [ ( a + 1 ) 2 i − 2 ( a + 1 ) i 2 + i 3 ] = 2 a ( a + 1 ) 3 − 3 a ( a + 1 ) 2 ( 2 a + 1 ) + [ 2 a ( a + 1 ) ] 2 = a ( a + 1 ) 2 [ 2 a + 1 − 3 2 a + 1 + 4 a ] = 1 2 a ( a + 1 ) 2 ( a + 2 )
Therefore, the total number of quadrilaterals in an a -tiered pixelated right arrow grid is 1 2 a ( a + 1 ) ( a + 2 ) ( a + 3 ) + 1 2 a ( a + 1 ) 2 ( a + 2 ) = 1 2 a ( a + 1 ) ( a + 2 ) ( a + 3 + a + 1 ) = 1 2 a ( a + 1 ) ( a + 2 ) ( 2 a + 4 ) = 6 a ( a + 1 ) ( a + 2 ) 2
Now, substituting a = 3 0 , we would get the answer 1 5 8 7 2 0 .