Missing Heptagon Jigsaw Puzzle Piece
Eleven pieces of a heptagon jigsaw puzzle are shown here, five in one figure, six in another.
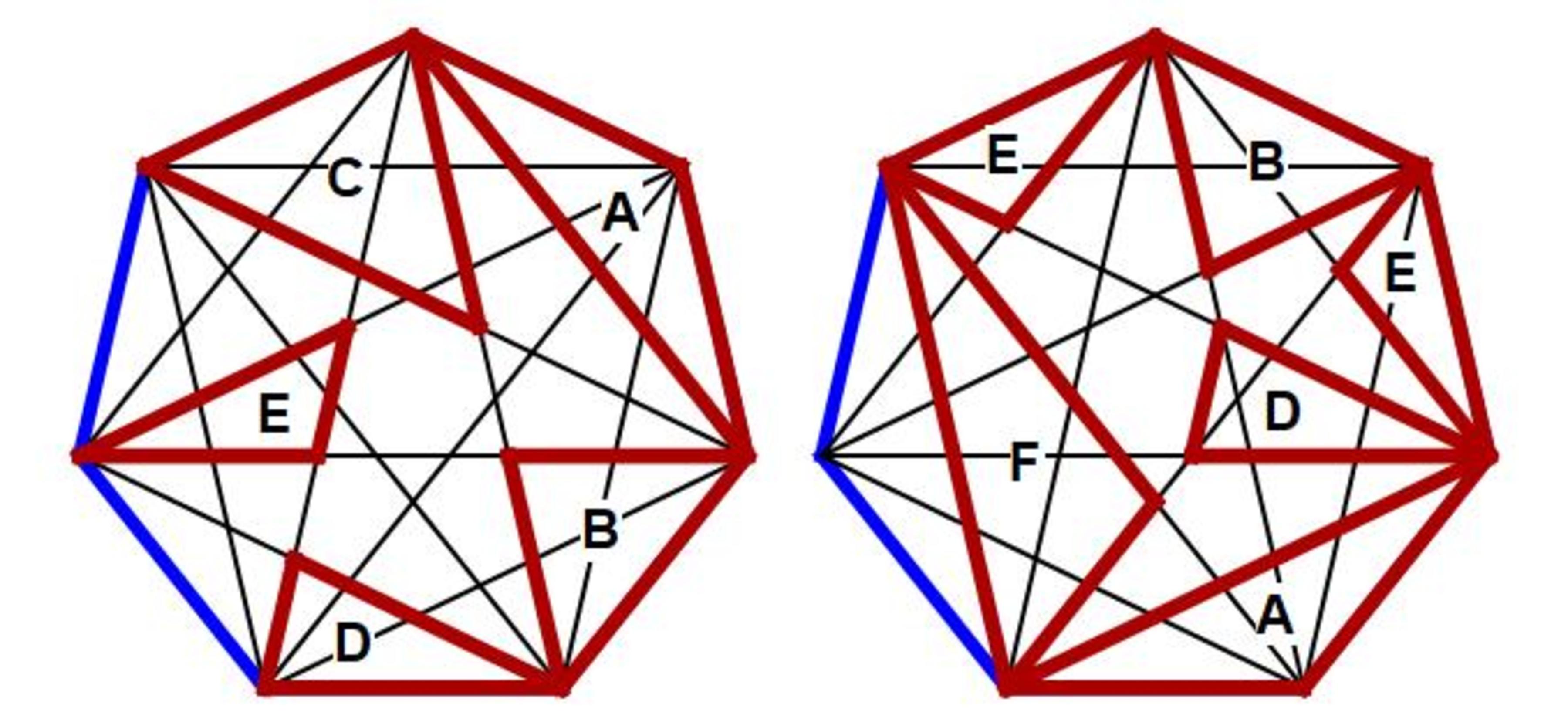
Combine the pieces to make up one heptagon of the same size as either. However, it takes twelve pieces to complete the jigsaw puzzle. One of the pieces are missing.
There are six kinds of triangular pieces, A , B , C , D , E , F . One more of one of them is needed. Which extra piece is that?
You may move around pieces and even flip them over.
The heptagon is a regular polygon, and diagonals are drawn for clarity, showing sizes and shapes of the pieces.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
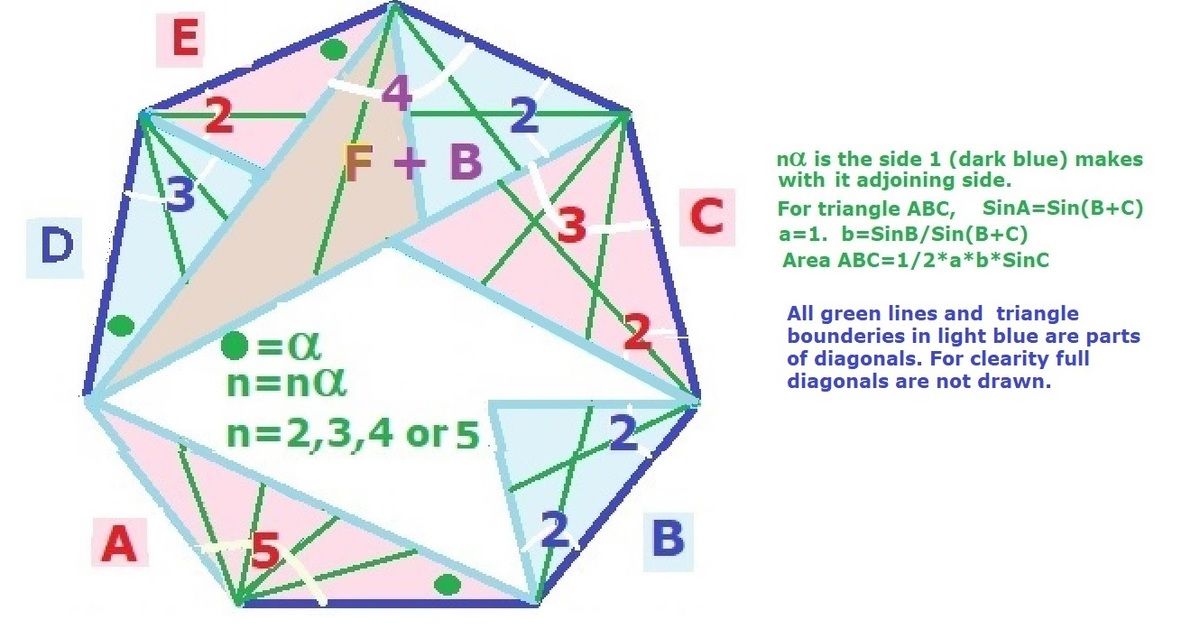
I n t h e n − g o n s , d i a g o n a l s f r o m a v e r t e x , f a n o u t a t e q u a l a n g l e s . T h e i n t e r n a l a n g l e h e r e = ( 7 − 2 ) ∗ 9 0 / 7 = 1 2 8 . 5 7 . A n g l e b e t w e e n a d j a c e n t d i a g o n a l s a n d b e t w e e n l a s t d i a g o n a l a n d s i d e i s 7 − 2 1 ∗ i n t e r n a l a n g l e = 5 1 ∗ 1 2 8 . 5 7 = 2 5 . 7 1 4 = s a y α . I f w e a s s u m e 7 − g o n s i d e = 1 , t h e v a r i o u s Δ s h a v e a n g l e s o n t w o s i d e s o f s i d e 1 , ( A − S − A ) i n α , a s c a n b e s e e n f r o m g i v e n F i g s , a n d n o t i n g t h a t F + B = 2 α − 1 − 4 α , A . . . . . 2 α − 1 − 5 α . . . . . . T h e r e a r e 2 A . . . . . . a r e a = 2 ∗ 0 . 3 9 0 9 , B . . . . . 2 α − 1 − 2 α . . . . . . T h e r e i s 1 B ( h e r e ) . . . . . . a r e a = 0 . 3 1 3 4 8 , C . . . . . 2 α − 1 − 3 α . . . . . . T h e r e i s 1 C . . . . . . a r e a = 0 . 4 8 7 4 5 , D . . . . . 1 α − 1 − 3 α . . . . . . T h e r e a r e 2 D . . . . . . a r e a = 2 ∗ 0 . 2 1 6 9 4 , E . . . . . 1 α − 1 − 2 α . . . . . . T h e r e a r e 3 E . . . . . . a r e a = 3 ∗ 0 . 1 7 3 9 7 , F + B . . . . . 2 α − 1 − 4 α . . . . . . ( O n e B h a s b e e n c o n s i d e r e d a b o v e ) . . . . . . a r e a = 0 . 8 7 8 2 7 . T h e t o t a l = 3 . 4 1 5 8 4 . A r e a o f u n i t 7 − g o n = 3 . 6 3 4 ∗ 1 2 . S o a r e a o f m i s s i n g t r i a n g l e = 3 . 6 3 4 − 3 . 4 1 6 = 0 . 2 1 8 , i t i s Δ D .
Here's another way to do this:
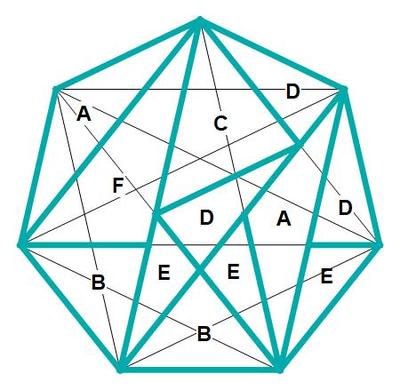
Here is one way to put the puzzle together with an extra D piece :
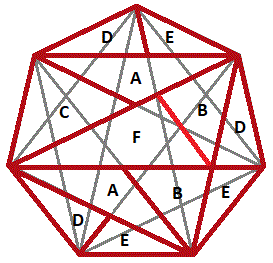
Thanks for posting a solution! I'll give my version.
I got fascinated with the "Golden Trisection" ratios found in the regular heptagon, but ended up developing this jigsaw puzzle for a problem. The "Golden Trisection" Ratio involves two constants, p , q , which are related by the following proportions:
1
:
p
:
q
p
:
1
+
q
:
p
+
q
q
:
p
+
q
:
1
+
p
+
q
This puzzle is full of such measures. The exact values of p , q are:
p = S i n ( 7 π ) S i n ( 7 2 π )
q = S i n ( 7 π ) S i n ( 7 4 π )
Log in to reply
I started by calculating all the areas of each triangle and was able to deduce that D was missing, but in the end I literally printed the puzzle out, cut the pieces, and assembled it on my dining room table.
Digvijay Singh had several problems dealing with these same angles, including this one and this one that you may find interesting.
I n t h e n − g o n s , d i a g o n a l s f r o m a v e r t e x , f a n o u t a t e q u a l a n g l e s . T h e i n t e r n a l a n g l e h e r e = ( 7 − 2 ) ∗ 9 0 / 7 = 1 2 8 . 5 7 . A n g l e b e t w e e n a d j a c e n t d i a g o n a l s a n d b e t w e e n l a s t d i a g o n a l a n d s i d e i s 7 − 2 1 ∗ i n t e r n a l a n g l e = 5 1 ∗ 1 2 8 . 5 7 = 2 5 . 7 1 4 = s a y α . I f w e a s s u m e 7 − g o n s i d e = 1 , t h e v a r i o u s Δ s h a v e a n g l e s o n t w o s i d e s o f s i d e 1 , ( A − S − A ) i n α , a s c a n b e s e e n f r o m g i v e n F i g s , a n d n o t i n g t h a t F + B = 2 α − 1 − 4 α , A . . . . . 2 α − 1 − 5 α . . . . . . T h e r e a r e 2 A . . . . . . a r e a = 2 ∗ 0 . 3 9 0 9 , B . . . . . 2 α − 1 − 2 α . . . . . . T h e r e i s 1 B ( h e r e ) . . . . . . a r e a = 0 . 3 1 3 4 8 , C . . . . . 2 α − 1 − 3 α . . . . . . T h e r e i s 1 C . . . . . . a r e a = 0 . 4 8 7 4 5 , D . . . . . 1 α − 1 − 3 α . . . . . . T h e r e a r e 2 D . . . . . . a r e a = 2 ∗ 0 . 2 1 6 9 4 , E . . . . . 1 α − 1 − 2 α . . . . . . T h e r e a r e 3 E . . . . . . a r e a = 3 ∗ 0 . 1 7 3 9 7 , F + B . . . . . 2 α − 1 − 4 α . . . . . . ( O n e B h a s b e e n c o n s i d e r e d a b o v e ) . . . . . . a r e a = 0 . 8 7 8 2 7 . T h e t o t a l = 3 . 4 1 5 8 4 . A r e a o f u n i t 7 − g o n = 3 . 6 3 4 ∗ 1 2 . S o a r e a o f m i s s i n g t r i a n g l e = 3 . 6 3 4 − 3 . 4 1 6 = 0 . 2 1 8 , i t i s Δ D .