Missing Link 4

Level pending

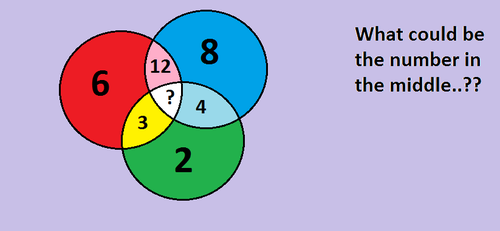What could be the number in the middle of all circles..??

#Misc

36 42 48 30

2 solutions

Aaditya Bhatt
Jul 15, 2014

Observe that number obtained by combining two colors is derived by multiplying both color and dividing it by 4.

Example. RED has number 6 and BLUE has number 8. So PINK color is derived as (6 * 8)/4 = 12.

And same way ultimate middle number is derived by multiplying all combined colors (12 * 4 * 3)/4 = 36.

Answer could also be 12. Half of each outside circle added together would give you the intersection. By that logic, the intersection of all 3 should be 4+3+1=12.

Jeron Blake - 6 years, 11 months ago

I think you should remove the word "prime" in "prime colors".

Ajala Singh - 6 years, 11 months ago

Could this problem be solvef by set theory

Divyansh Mundra - 6 years, 10 months ago

ambigitious answers guess this one

math man - 6 years, 10 months ago

If the answer in the intersection is based on multiplying the base circle numbers together and dividing by 4, then by that logic the centre number should be 2x6x8/4 = 24. Surely it's the base numbers that should be used again here not the 2-circle numbers?

Rachel Sheridan - 6 years, 10 months ago

G C Keerthi Vasan
Jul 17, 2014

observe that..

$12*3$ mod10 =6

$12*4$ mod10=8

$3*4$ mod10= 2

therefore the missing number say x must also satisfy the conditions:

$12*3* x$ mod(10)=6

$12*4* x$ mod(10)=8

$3*4* x$ mod(10)=2

it is conclusive that x must end in 6 for all the above statements to be true..

therefore the only option ending in 6 is 36.

hence the answer

Even if x=1, equations are satisfied ? It will have no effect on final answer.

Niranjan Khanderia - 6 years, 10 months ago

x is any integer other than 1! because you take one then.. you get the same initial value again!

G C KEERTHI Vasan - 6 years, 10 months ago

Missing Link 4

2 solutions

0 pending reports