Missing Radius

Label the diagram as follows:

Let the sides of each square be $s = CD = BC$ . Since $\triangle ACD$ is a right isosceles triangle, $AC = \frac{s}{\sqrt{2}}$ .

By the law of cosines on $\triangle ABC$ , $AB^2 = BC^2 + AC^2 - 2 \cdot BC \cdot AC \cdot \cos 135°$ , or $R^2 = s^2 + (\frac{s}{\sqrt{2}})^2 - 2 \cdot s \cdot \frac{s}{\sqrt{2}} \cdot (-\frac{1}{\sqrt{2}})$ , or $R = \sqrt{\frac{5}{4} \cdot 2 s^2}$ .

Since the area of both square is $2021$ , $2s^2 = 2021$ , so $\lfloor R \rfloor = \lfloor \sqrt{\frac{5}{4} \cdot 2021} \rfloor = \boxed{50}$ .

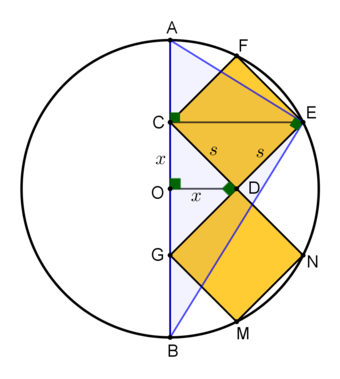Following the labelling of the figure, denote $OD$ and $CD$ by $x$ and $s$ respectively.
Obviously, the two squares are congruent, since $\triangle CDG$ is isosceles, thus ${{s}^{2}}=\dfrac{2021}{2}$ .
By Pythagoras’s theorem on right triangles $\triangle OCD$ , $\triangle CDE$ we have $2{{x}^{2}}={{s}^{2}}\text{ and }C{{E}^{2}}=2{{s}^{2}}$ Moreover, $\triangle AEB$ is a right triangle as well and $CE$ is its height on the hypotenuse, thus

$\begin{aligned} C{{E}^{2}}=CA\cdot CB & \Rightarrow 2{{s}^{2}}=\left( R-x \right)\cdot \left( R+x \right) \\ & \Rightarrow 2{{s}^{2}}={{R}^{2}}-{{x}^{2}} \\ & \Rightarrow {{R}^{2}}=2{{s}^{2}}+\frac{{{s}^{2}}}{2} \\ & \Rightarrow {{R}^{2}}=\frac{5}{2}{{s}^{2}} \\ & \Rightarrow {{R}^{2}}=\frac{5}{2}\cdot \frac{2021}{2} \\ & \Rightarrow R=\frac{\sqrt{10105}}{2}\approx \text{50}\text{.26} \\ \end{aligned}$ For the answer, $\left\lfloor R \right\rfloor =\boxed{50}$ .

Let the side of square is $a$ :

$\begin{aligned} a &= \sqrt {\dfrac {2021}{2}} \\ R &= \sqrt {\left (\dfrac {a}{\sqrt 2} \right )^2 + (\sqrt 2 a)^2} = \dfrac{\sqrt 5}{\sqrt 2} a \\ &= \dfrac{\sqrt 5}{\sqrt 2} \sqrt {\dfrac {2021}{2}} \approx 50.26 \\ \therefore \lfloor R \rfloor &= 50 \end{aligned}$