Missouri's Reducible Fractions
Find 1 0 positive fractions each written in lowest terms, each of which is strictly less than 1 and any two are distinct, such that:
- The product of all 1 0 fractions equals 1 0 1 ;
- The product of 9 of these 1 0 equals 9 1 ;
- The product of 8 of these 1 0 equals 8 1 ; ⋮ ⋮ ⋮ ⋮
- The product of 3 of these 1 0 equals 3 1 ;
- The product of 2 of these 1 0 equals 2 1 ;
- The denominators of all these 1 0 fractions do not exceed 1 0 .
It can be shown that if S denote the sum of unordered solution of these 1 0 fractions, then the sum of all distinct S can be expressed as B A for coprime positive integers A and B . Input A + B as your answer.
This is originally Eastern Illinois University Math Challenge problem, which is directed from Missouri State challenge problems.
The answer is 21397.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
For completeness, for the first set of solution:
3 2 , 4 3 , 5 4 , 6 5 , 7 5 , 7 6 , 8 7 , 9 8 , 1 0 7 , 1 0 9
1 / 2 1 / 3 1 / 4 1 / 5 1 / 6 1 / 7 1 / 8 1 / 9 1 / 1 0 = = = = = = = = = 2 / 3 × 3 / 4 = 5 / 7 × 7 / 1 0 2 / 3 × 5 / 7 × 7 / 1 0 2 / 3 × 3 / 4 × 5 / 7 × 7 / 1 0 2 / 3 × 3 / 4 × 4 / 5 × 5 / 7 × 7 / 1 0 2 / 3 × 3 / 4 × 4 / 5 × 5 / 6 × 5 / 7 × 7 / 1 0 2 / 3 × 3 / 4 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 1 0 2 / 3 × 3 / 4 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 1 0 × 7 / 8 2 / 3 × 3 / 4 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 1 0 × 7 / 8 × 8 / 9 2 / 3 × 3 / 4 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 1 0 × 7 / 8 × 8 / 9 × 9 / 1 0
And for the second set of solution:
4 3 , 5 3 , 5 4 , 6 5 , 7 5 , 7 6 , 8 7 , 9 7 , 9 8 , 1 0 9
1 / 2 1 / 3 1 / 4 1 / 5 1 / 6 1 / 7 1 / 8 1 / 9 1 / 1 0 = = = = = = = = = 3 / 5 × 5 / 6 3 / 5 × 5 / 7 × 7 / 9 3 / 4 × 3 / 5 × 5 / 7 × 7 / 9 3 / 4 × 3 / 5 × 4 / 5 × 5 / 7 × 7 / 9 3 / 4 × 3 / 5 × 4 / 5 × 5 / 6 × 5 / 7 × 7 / 9 3 / 4 × 3 / 5 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 9 3 / 4 × 3 / 5 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 9 × 7 / 8 3 / 4 × 3 / 5 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 9 × 7 / 8 × 8 / 9 3 / 4 × 3 / 5 × 4 / 5 × 5 / 6 × 5 / 7 × 6 / 7 × 7 / 9 × 7 / 8 × 8 / 9 × 9 / 1 0
That'll explain why I couldn't prove uniqueness! It's extraordinary that there are precisely two solutions.
Say the fractions are, in some order, x 1 , x 2 , … , x 1 0 . Obviously there are lots of ways we could pick, say, the five fractions whose product has to be one fifth ( 2 5 2 ways, to be exact), so in most cases we can't immediately assign the fractions to their given products in most cases; but let's be more optimistic. We can say that i = 1 ∏ 1 0 x i = 1 0 1
and, since we can choose the labelling of the x i , we can have i = 1 ∏ 9 x i = 9 1
Comparing these, we get x 1 0 = 1 0 9 . In fact, if we assume that the fractions not included in the next product are x 9 , x 1 0 , we'd get i = 1 ∏ 8 x i = 8 1
and x 9 = 9 8 . It's clear that we can keep going like this, following the pattern x i = i i − 1 for i > 1 .
Of course, now we see the problem: if x 2 = 2 1 , we would need x 1 = 1 , which - although it would satisfy all the required products - is not allowed in the conditions.
Remaining optimistic (if a bit less so), let's instead say that x i = i i − 1 for i > 2 , and seek a pair of fractions x 1 , x 2 not already in this list such that x 1 x 2 = 2 1 .
Say that x 1 = q p and x 2 = s r , where p , q , r , s are positive integers and the fractions are in lowest terms. Then we need 2 p r = q s , 1 < q ≤ s ≤ 1 0 (where again we're free to choose q ≤ s .) We also need p < q − 1 and r < s − 1 , so as not to clash with one of the x i we've already chosen.
It's a bit of casework but not too hard to show that the unique pair of fractions satisfying these conditions are x 1 = 7 5 and x 2 = 1 0 7 . The complete list of fractions is then 7 5 , 1 0 7 , 3 2 , 4 3 , 5 4 , 6 5 , 7 6 , 8 7 , 9 8 , 1 0 9 and it's easy to verify that the product of the first n fractions in this list is n 1 .
The sum of these fractions is 2 5 2 0 2 0 1 2 3 .
Note that this approach finds a set of fractions that works, but doesn't prove uniqueness (we made an assumption in calculating x 9 but it doesn't rule out other possibilities).
We have a product of 2 distinct proper fractions that is equal to 1 0 1 ÷ 8 1 = 5 4 .
Let these two fractions be b a and d c , where 1 ⩽ a < b ⩽ 1 0 , 1 ⩽ c < d ⩽ 1 0 , g cd ( a , b ) = g cd ( c , d ) = 1 , b a = d c
If we exhaustively search for all such integers, we can conclude that two of these ten fractions are 9 8 and 1 0 9 .
Say that x 1 = q p and x 2 = s r , where p , q , r , s are positive integers and the fractions are in lowest terms. Then we need 2 p r = q s , 1 < q ≤ s ≤ 1 0 (where again we're free to choose q ≤ s .) We also need p < q − 1 and r < s − 1 , so as not to clash with one of the x i we've already chosen.
It's a bit of casework but not too hard to show that the unique pair of fractions satisfying these conditions are x 1 = 7 5 and x 2 = 1 0 7 .
This isn't necessarily true. Note that in my second set of solution, none of the fractions chosen is equal to 1 0 7 . Plus, what's stopping us from choosing another pair of fractions such that their product is 2 1 as well?
Also, ( 7 5 , 1 0 7 ) is not the only pair of proper fractions that satisfy the 9 th bullet point.
The other pairs that doesn't clash with the earlier x i 's chosen are:
( 3 2 , 4 3 ) , ( 5 3 , 6 5 ) , ( 5 4 , 8 5 ) , ( 7 4 , 8 7 )
Log in to reply
Er...all of those pairs have a clashing fraction! Remember the "earlier chosen x i s" in my solution are the fractions of the form x i = i i − 1 for i = 3 , 4 , … , 1 0 , ie 3 2 , 4 3 , 5 4 , 6 5 , 7 6 , 8 7 , 9 8 , 1 0 9
In the four pairs you list, you have clashes with 3 2 and 4 3 in the first one, 6 5 in the second, 5 4 in the third and 8 7 in the fourth.
The point - not that there was much of a point - to my solution was that the naïve approach of trying to construct the set of x i in the simplest way works. No reordering of the x i is needed; they satisfy i = 1 ∏ n x i = n 1 for n > 1 .
I'm pretty sure the set I found is the unique with this property. However, as you showed, it's not the unique set answering the original question. (Note though that your second set doesn't have the property above.)
This was the only way I could think of to find a solution by hand - I'm still not sure whether that was a requirement in the inspiration for this question.
Log in to reply
Ah my apologies. I made the same wishful thinking about generating these fractions via x i = 1 − i 1 but I couldn't justify why the first set of solution works. And I tried to prove its uniqueness. But as you can see, it failed spectacularly.
I've updated my solution. You might be interested to see that with barely any casework, we can deduce that 5 of the 1 0 fractions must be the 5 largest permissible fractions possible:
{ 6 5 , 7 6 , 8 7 , 9 8 , 1 0 9 }
Log in to reply
Wow, that's a great insight in your update. Now you've got this perhaps it's possible to solve the rest by hand too? It really limits the options. Consider how to make 2 1 as the product of two fractions. With all denominators less than 1 1 , the only way we can use fractions from this list is as one of 6 5 ⋅ 5 3 , 8 7 ⋅ 7 4 , 1 0 9 ⋅ 9 5
Without using any of these fractions, we can have 3 2 ⋅ 4 3 , 5 4 ⋅ 8 5 , 7 5 ⋅ 1 0 7
In the first case we get 6 of the full set of fractions, and know the product of the other 4 ; in the second case we know 7 and the product of the other 3 . Still quite a bit of case analysis to go, though.
Log in to reply
Sorry, make that 6 of 10, not 5 of 10:
{ 5 4 , 6 5 , 7 6 , 8 7 , 9 8 , 1 0 9 }
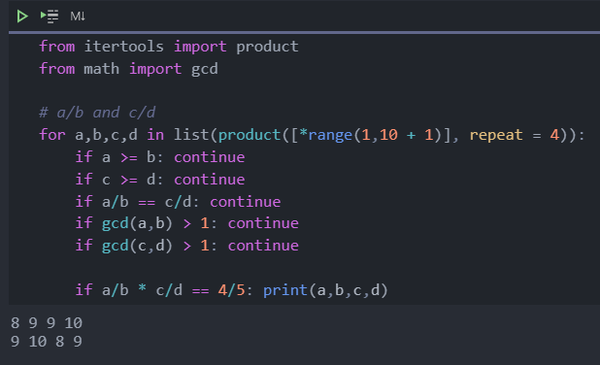
Next, let's figure out the number of such proper fractions whose denominators are at most 1 0 . A simple script tells us that there are 2 5 such proper fractions:
0
There is a total of ( 1 0 2 5 ) = 3 , 2 6 8 , 7 6 0 ways to select 1 0 of these fractions. To add to that, for each of these 1 0 -tuplets, we have to verify that they satisfy all the bullet points. That's quite a daunting task!
In order to reduce the number of cases to check, we will attempt to narrow down which of these 2 5 fractions must be chosen.
Confirmation:
0
0
Thus, the two solutions are:
Let's verify that these 2 solutions satisfy all the given bullet points.
0
The answer follows.
0
What's incredible is that the results produced from the scripts are all instantaneous!