Mobile robot 1
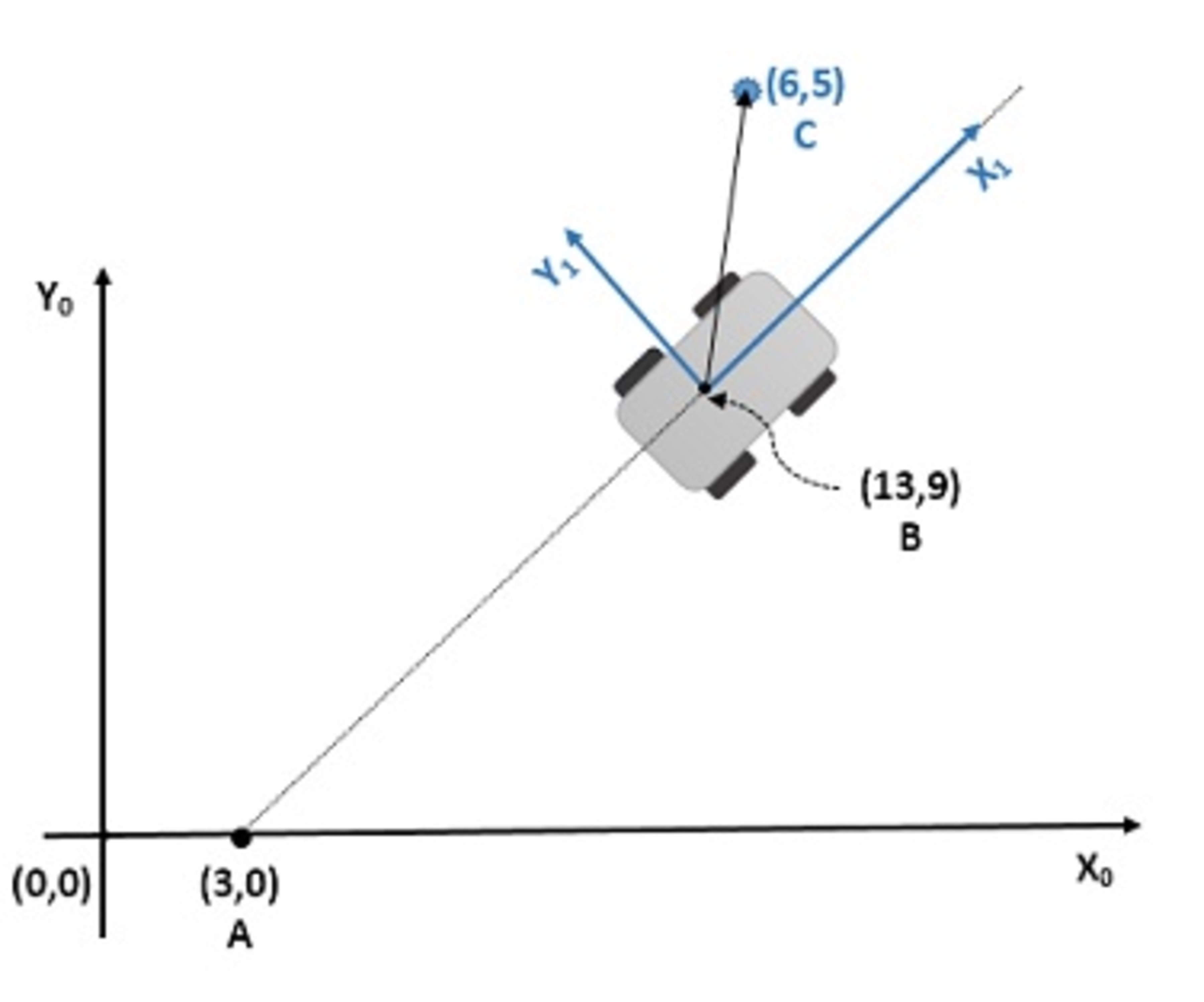
A mobile robot, with a reference frame ( x 0 , y 0 ) assigned as shown in the above figure, is on a planar track and moves from point A = ( 3 , 0 ) in a linear path to point B = ( 1 3 , 9 ) .
When the robot arrives to point B , the mobile robot’s sensors detect a small object located at C = ( 6 , 5 ) , w.r.t its coordinates ( x 1 , y 1 ) Find the coordinates of this object w.r.t. the reference frame ( x 0 , y 0 ) .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is a very nice approach to solving the problem.
Log in to reply
Thanks. I assume there is going to be a Part 2 coming?
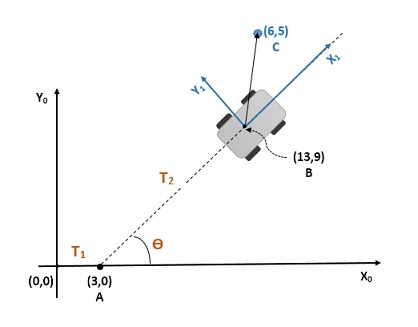
You may solve this by using rotation and translation [ 4 × 4 ] homogenous matrices.
As shown in the above figure, there two Transformations T 1 and T 2 , where
T 1 = translation matrix from point ( 0 , 0 ) to point ( 3 , 0 ) = ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 1 0 0 0 0 1 0 3 0 0 1 ⎠ ⎟ ⎟ ⎞
T 2 = translation matrix from point ( 3 , 0 ) to point ( 1 3 , 9 ) followed by rotation of ∠ θ = ⎝ ⎜ ⎜ ⎛ cos ( θ ) sin ( θ ) 0 0 − sin ( θ ) cos ( θ ) 0 0 0 0 1 0 1 0 9 0 1 ⎠ ⎟ ⎟ ⎞
∠ θ = rontation angle about z − a x i s by ∠ tan − 1 ( 1 0 9 ) and sin ( θ ) = 1 8 1 9 & cos ( θ ) = 1 8 1 1 0
Then the total transformation T = T 1 T 2 = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 8 1 1 0 1 8 1 9 0 0 − 1 8 1 9 1 8 1 1 0 0 0 0 0 1 0 1 3 9 0 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
Any point expressed in frame ( x 1 , y 1 ) can be expressed in frame ( x 0 , y 0 ) by using the transformation matrix T
Point C in frame ( x 0 , y 0 ) = T [ C expressed in frame ( x 1 , y 1 ) ] = T ⎝ ⎜ ⎜ ⎛ 6 5 0 1 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 8 1 6 0 − 1 8 1 4 5 + 1 3 1 8 1 5 4 + 1 8 1 5 0 + 9 0 1 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 4 . 1 1 5 1 6 . 7 3 0 0 1 ⎠ ⎟ ⎟ ⎞
Define the vector from A to B:
v A B = ( 1 3 − 3 ) ı ^ + ( 9 − 0 ) ȷ ^ = 1 0 ı ^ + 9 ȷ ^
The first unit vector of a pair of orthogonal unit vectors that will define the new coordinate system:
u 1 = 1 8 1 1 0 ı ^ + 9 ȷ ^
And the second:
u 2 = 1 8 1 − 9 ı ^ + 1 0 ȷ ^
The displacement of the small object from the origin in the original coordinate system is:
D x = 1 3 + 6 u 1 x + 5 u 2 x = 1 3 + 1 8 1 6 0 − 1 8 1 4 5 ≈ 1 4 . 1 1 5 D y = 9 + 6 u 1 y + 5 u 2 y = 9 + 1 8 1 5 4 + 1 8 1 5 0 ≈ 1 6 . 7 3 0