Mode of remainders
Number Theory
Level
4
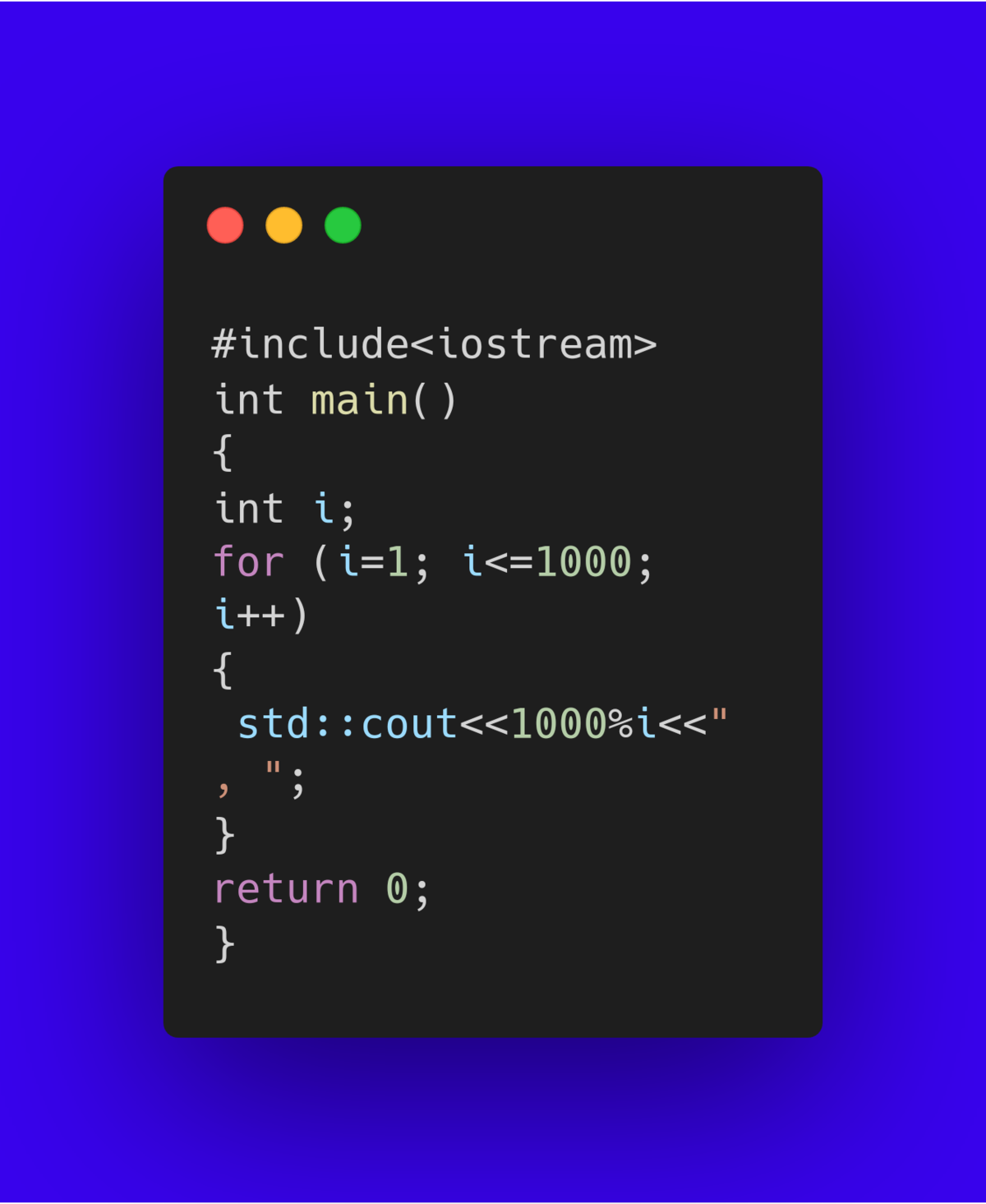
Divide 1000 by each integer from 1 to 1000 and record their remainders.
Among the 1000 remainders recorded, what number do you see most frequently?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

For any possible remainder 0 ≤ r ≤ 9 9 9 , the number 1 0 0 0 gives remainder r when divided by 1 ≤ n ≤ 1 0 0 0 exactly when n > r and n divides 1 0 0 0 − r . Thus the frequency f r of the remainder r is equal to the number of divisors of 1 0 0 0 − r which are greater than r .
Now 1 0 0 0 − 1 0 = 9 9 0 = 2 × 3 2 × 5 × 1 1 has 2 × 3 × 2 × 2 = 2 4 positive divisors. Of these, 1 , 2 , 3 , 5 , 6 , 9 , 1 0 are less than or equal to 1 0 . Thus we deduce that f 1 0 = 1 7 . We want to determine whether there are any other integers 0 ≤ r ≤ 9 9 9 with f r ≥ 1 7 . Note that 1 0 0 0 = 2 3 × 5 3 has 4 × 4 = 1 6 positive divisors, and so f 0 = 1 6 . Also, since 9 9 9 = 3 3 × 3 7 , we have that f 1 = 4 × 2 − 1 = 7 .
Suppose now that r ≥ 6 0 . If 1 ≤ m ≤ 1 0 0 0 is such that m > r and m divides 1 0 0 0 − r , then m 1 0 0 0 − r < r 1 0 0 0 − r = r 1 0 0 0 − 1 ≤ 6 0 1 0 0 0 − 1 < 1 6 Thus the integer m 1 0 0 0 − r can take at most 1 5 values, which means that there are at most 1 5 possible values of m . In other words f r ≤ 1 5 .
If 2 ≤ r ≤ 5 9 and f r ≥ 1 7 then (since 1 divides 1 0 0 0 − r ) we must have that 1 0 0 0 − r has at least 1 8 positive divisors. There are only four numbers 2 ≤ r ≤ 5 9 such that 1 0 0 0 − r has 1 8 or more positive divisors: 1 0 , 2 0 , 2 8 , 4 0 .
Thus the mode is 1 0 .
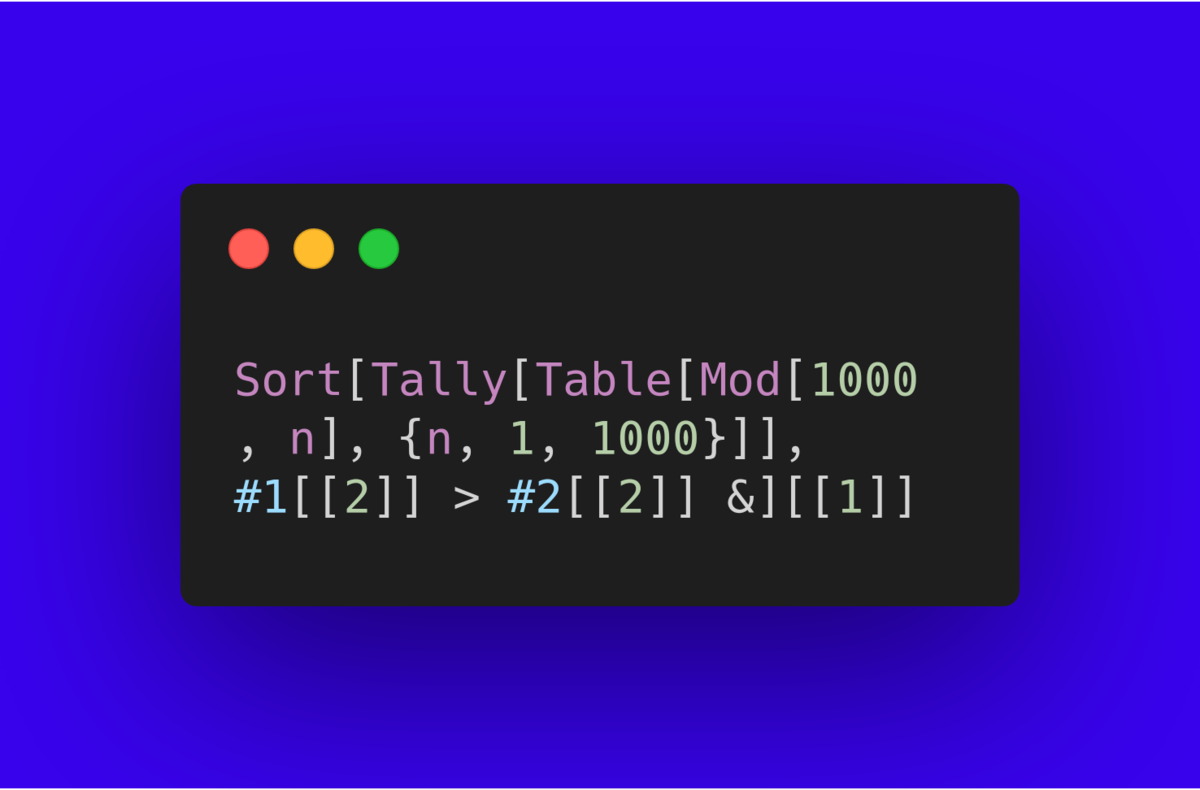
Alternatively, the Mathematica command:
yields
giving the same answer!