Model of a 1-dimensional gas
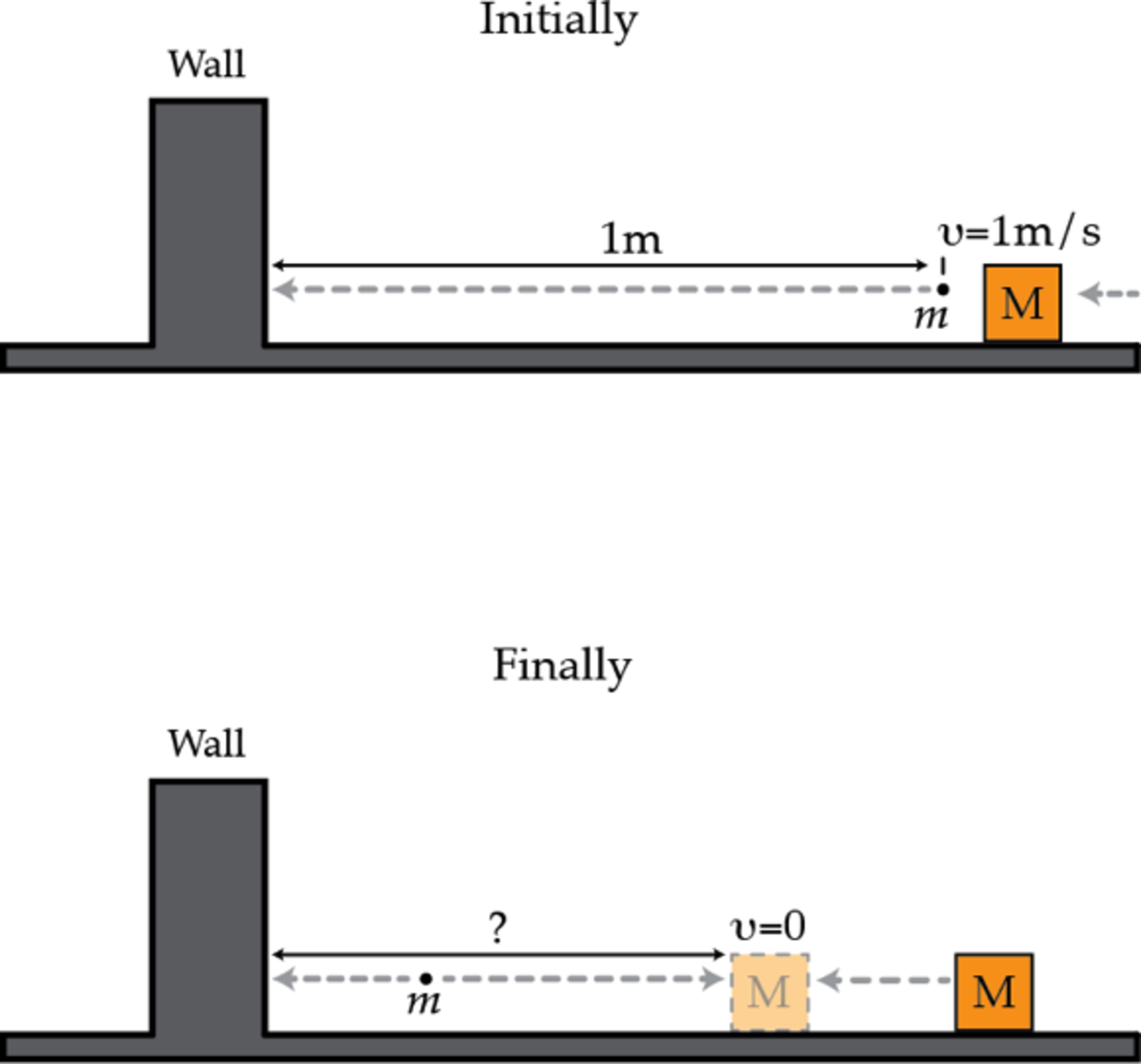
A block with mass M and speed V 0 = 1 m/s , slides on a frictionless surface towards a fixed wall. The block strikes a small particle with mass m , initially at rest at a distance L 0 = 1 m from the wall. The particle bounces elastically off the block then slides to the wall where it bounces elastically and then slides back to the block. The particle continues to bounce elastically back and forth between the block and the wall. It turns out that the block won't reach the wall. This is because the small particle can be treated as a 1-dimensional gas being compressed adiabatically. Thus, as the volume of this "gas" decreases, its pressure increases and the block eventually comes to a stop. If m M = 3 × 1 0 4 , how close in millimeters does the block come to the wall?
The answer is 5.77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Suppose that right after the kth collision the block and the particle have speeds V k and u k , respectively, and are at a distance L k from the wall. The particle slides to the wall and slides back to the block. The equations expressing the conservation of linear momentum and kinetic energy in the k+1th collision are: 2 M V k + 1 2 + 2 m u k + 1 2 = 2 M V k 2 + 2 m u k 2 M V k + 1 + m u k + 1 = M V k − m u k These two equations allow us to express V k + 1 and u k + 1 in terms of V k and u k . In particular, it is easy to show that V k + V k + 1 = u k + 1 − u k . If t k is the time between the kth and k+1th collisions the 2 L k = V k t k + u k t k and L k + 1 = L k − V k t k . From the last three relations we find that L k + 1 ( u k + 1 − V k + 1 ) = L k ( u k − V k ) . In other words, L k ( u k − V k ) is an invariant. We can exploit the invariance of this quantity to find the minimum distance between the block and the wall. When the block reaches its closest point to the wall, all its kinetic energy is transferred to the particle. Then i n v = L k f i n a l ( u k f i n a l − V k f i n a l ) = L m i n m M v 0 . The value of invariant inv can be determined from the initial conditions of the problem. Right after the first collision we have that L 1 = L 0 and u 1 − V 1 = V 0 . Thus L m i n = M m L 0 = 5 . 7 7 mm . Note that this result is only valid when M ≫ m . We have tacitly assumed that the velocity of the block is zero when when it reaches the closest point to the wall. This is a plausible assumption only in the regime M ≫ m . Then, the speed of the box decreases gradually after each collision with the particle and the block practically stops when L = L m i n .
did the same
we all know that
d
E
=
Q
+
W
and in the adiabatic process Q =0 that yields
d
E
=
W
so
=
n
C
v
Δ
T
then when the second collision happen the transferred Kinetic energy is the energy transferred in the first one and the second one so
e
q
(
1
)
2
1
m
(
(
2
V
o
)
2
)
+
2
1
m
(
(
2
V
o
)
2
)
=
n
C
v
Δ
T
and according to the adiabatic process Law
P
V
γ
=
P
o
V
o
γ
we yield that
P
(
A
x
)
γ
=
P
o
V
o
γ
so
P
=
P
o
(
A
A
x
1
)
γ
where
A
x
is the instant volume , and according to the ideal gas law
P
V
=
n
R
T
we conclude that
T
=
n
R
P
V
, putting in the eq(1)
we yield that
2
2
1
m
(
(
2
V
o
)
2
)
=
n
C
v
(
n
R
P
V
−
n
R
P
o
V
o
)
so
m
(
(
2
V
o
)
2
)
=
n
C
v
(
n
R
P
V
−
n
R
P
o
V
o
)
then
4
m
V
o
2
=
n
C
v
(
n
R
P
V
−
n
R
P
o
V
o
)
so
4
m
V
o
2
=
n
C
v
n
R
P
o
V
o
(
−
1
+
x
(
γ
−
1
)
1
)
note that the
C
v
for a one dimensional gas is
2
1
R
so
γ
=
3
and note that the second collision happens when
x
=
3
1
so
4
m
V
o
2
=
2
P
o
V
o
(
−
1
+
x
γ
1
x
)
then when
x
=
3
1
so
4
m
V
o
2
=
2
P
o
V
o
(
−
1
+
3
3
1
1
x
)
that yields
P
o
V
o
=
m
in the last collision the whole Kinetic energy for M is transferred into internal energy of the gas so
Δ
E
=
2
m
(
−
1
+
x
2
1
)
so
2
1
M
V
o
2
=
2
m
(
−
1
+
x
2
1
)
so
M
V
o
2
=
m
(
−
1
+
x
2
1
)
so
m
M
=
−
1
+
x
2
1
then
m
M
+
1
=
x
2
1
that yields
m
M
+
1
1
=
x
2
finaly
x
=
(
m
M
+
1
)
2
1
1
so
x
=
5
.
7
7
m
m
It is the same as main
The block and the particle go through several elastic collisions before the block moves in the opposite direction. Because these collisions are discreet and independent of each other, it is a good idea to use Euler's Method for this problem.
Since we are not given the mass of either M or m, we can assume that m = 1 kg and that M = 30000 kg. Let V n and v n represent the velocity (without regard to direction) of the block and the particle respectively after the n t h collision. We are given that V 0 = 1 m/s and v 0 = 0 m/s.
We know that V n + 1 = M + m V n ( M − m ) + 2 m v n and v n + 1 = M + m v n ( M − m ) + 2 M V n from the formulas for elastic collisions.
Let p n be the position of the n t h collision. We are given that p 1 = 1 .
We can derive p n from the variables p n − 1 , V n − 1 , and v n − 1 . We get that p n = v n − 1 + V n − 1 p n − 1 ( v n − 1 − V n − 1 ) .
We know all the information about the future collisions, so we can use Euler's method now. Our result is that the block is 5.77 mm away from the wall after 137 collisions.