Moderate 2015

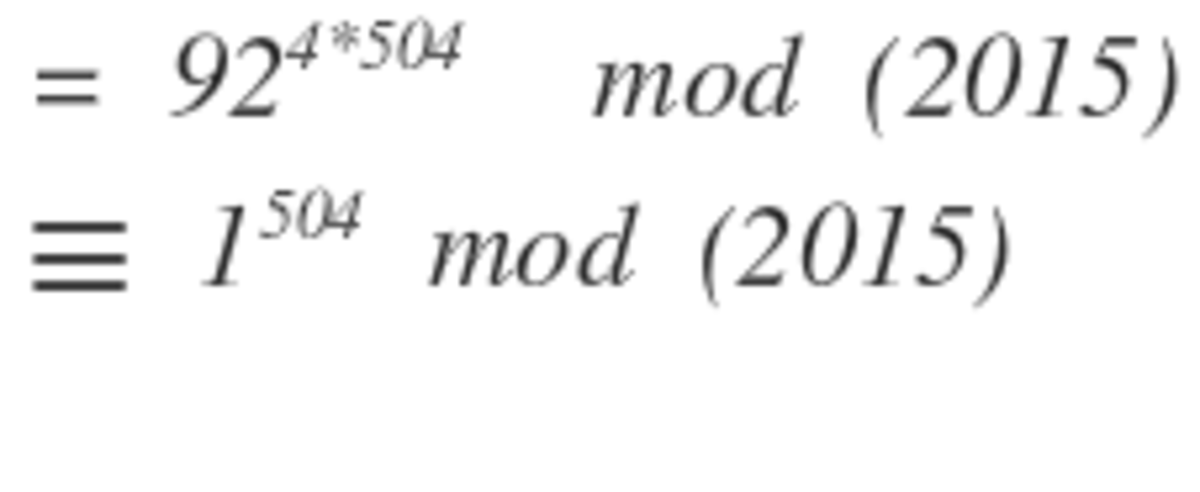
Since $2015 = 5 \times 13 \times 31,$ we can check $92^{2016}$ modulo 5, 13, and 31 separately. Since $92 = 31 \times 3 - 1 = 13 \times 7 + 1,$ we have

$92^{2016} \equiv (-1)^{2016} \equiv 1 \! \! \! \! \pmod{31}$

and

$92^{2016} \equiv 1^{2016} \equiv 1 \! \! \! \! \pmod{13}.$

Since $\gcd(92, 5) = 1,$ by Fermat's Little Theorem,

$92^{2016} \equiv (92^4)^{504} \equiv 1^{504} \equiv 1 \! \! \! \! \pmod{5} .$

Because $92^{2016}$ is 1 modulo 5, 13, and 31, it must also be $\boxed{1}$ modulo 2015, so that is our answer.

(Posting solutions to 3 year old problems FTW $\ddot \smile$ )