Modified YDSE!

Classical Mechanics Level 5

A Young's Double Slit Experiment (YDSE) is performed. In the figure, the light is entering from water with refractive index $\dfrac{4}{3}$ . There is a rectangular slab in front of $S_2$ which is filled with water.

Find the vertical position of central maxima.

Details and Assumptions:

Monochromatic light is used.
$d=0.3 \text{ mm}$
Thickness of slab $t=0.41\text{ mm}$ .
$D=1\text{ m}$ .
Consider the center of $S_1$ and $S_2$ to be the origin and the vertical distance being measured from it.
Use SI units.

The answer is 0.211.

1 solution

Gautam Sharma
Feb 22, 2016

Writing path difference w.r.t Air: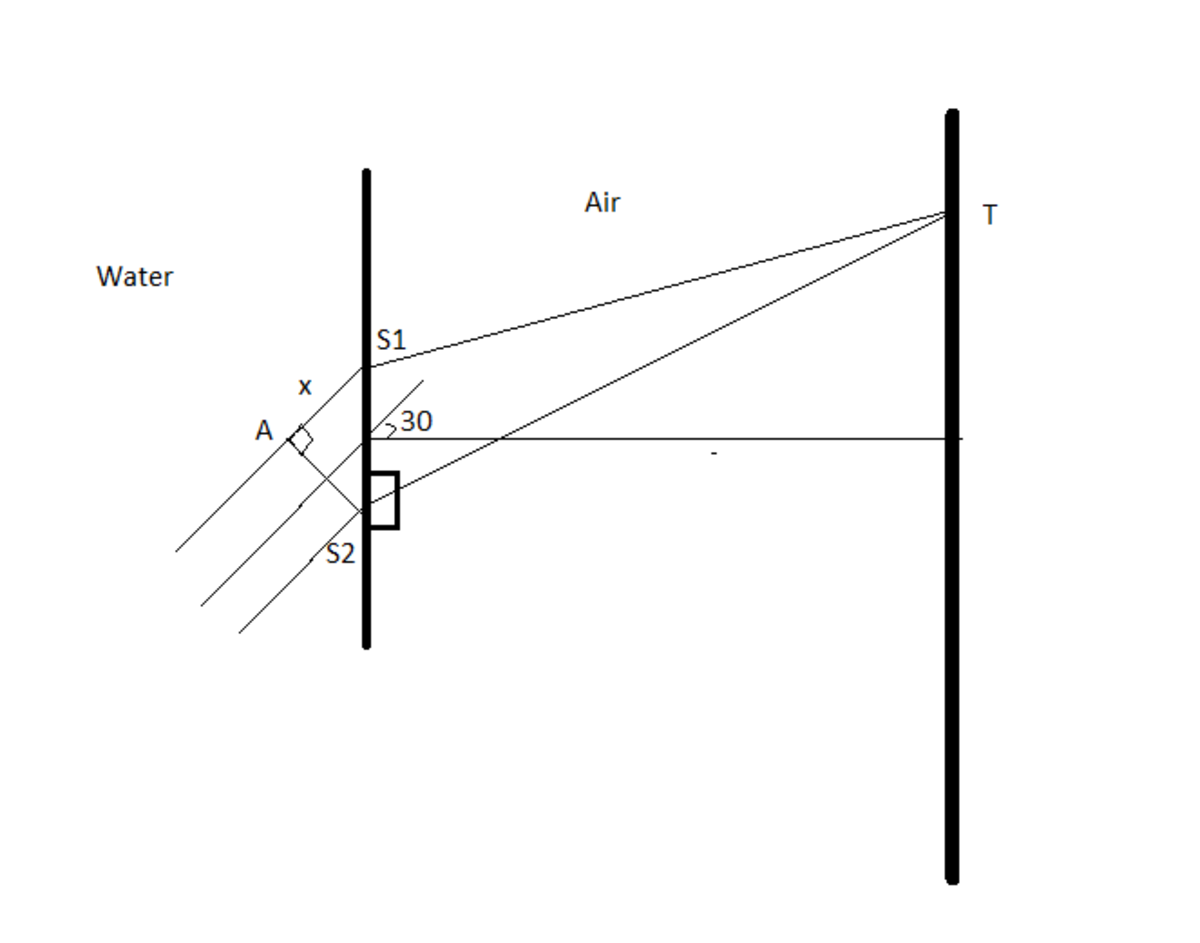

Below Ray path - Upper ray path

Simple geometrical path difference( $S_2T-S_1T$ )+Path difference due to slab(( $\mu -1)t$ ) -Extra Path of upper wave in water(x) .

$\Delta x =S_2T-S_1T+t(\mu_{slab} -1)-(\mu _w dsin30)$ $\Delta x= \frac{yd}{D}+t(\mu_{slab} -1)-(\mu _w dsin30)$

For Central maxima $\Delta x =0$ So $y=\frac{D[(\mu _w dsin30)-t(\mu_{slab} -1)]}{d}$

Putting values we can get the required answer.

Modified YDSE!

The answer is 0.211.

1 solution

0 pending reports