Modulus

Algebra Level 3

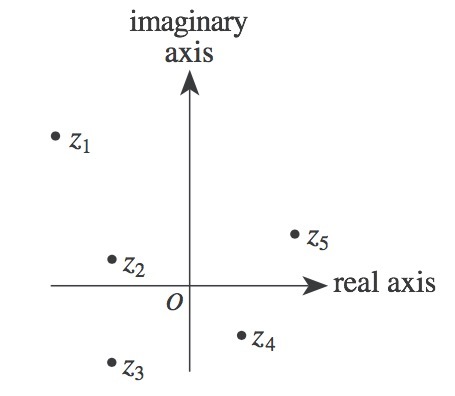
In the complex plane ,the horizontal axis is called the real axis and the vertical axis is called the imaginary axis. The complex number $a$ + $bi$ graphed in the complex plane is comparable to the point $(a,b)$ graphed in the standard $(x,y)$ coordinate plane. The modulus of the complex number $a$ + $bi$ is given by $\sqrt{a^{2} + b^{2}}$ . Which of the given complex numbers $z_{1}$ , $z_{2}$ , $z_{3}$ , $z_{4}$ and $z_{5}$ has the greatest modulus?

z_{4}

z_{3}

z_{2}

z_{5}

z_{1}

1 solution

Harsh Khatri
Mar 7, 2016

The modulus of a complex number is nothing but the distance of the point representing it in the complex plane, from the origin.

From the graph, it is seen that $z_1$ is the farthest from origin. Hence, it has the greatest modulus.

Modulus

1 solution

0 pending reports