Molar Heat capacity

Classical Mechanics Level 5

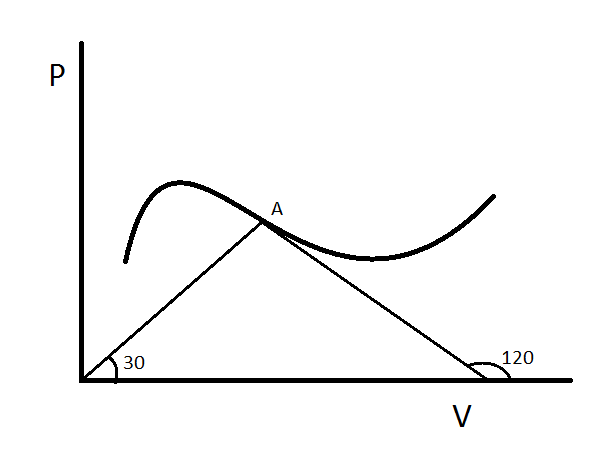
1 1 Mole of an Ideal monoatomic gas undergoes a process depicted in the figure. At some point A of the P − V P-V diagram line joining the A to origin makes an angle 30 30 degrees with the V V axis and the tangent at point A makes an angle 120 120 degrees with the V V axis.

Find the instantaneous molar heat capacity of gas at point A in c a l m o l − 1 K − 1 cal mol^{-1} K^{-1} Take R = 2 c a l m o l − 1 K − 1 R=2 cal mol^{-1} K^{-1}


The answer is 2.

Ishan Tarunesh by Ishan Tarunesh , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rohit Shah
Mar 27, 2015

Easy problem ! F r o m g r a p h , P = V 3 . . . ( 1 ) a n d d P d V = − 3 . . ( 2 ) S i n c e P V = n R T P d V + V d P = n R d T N o w u s i n g 1 a n d 2 a n d s o m e s i m p l e m a i n p u l a t i o n , P d V = − n R d T 2 d U = 3 2 n R d T d q = d U + d W d q = n R d T M o l a r h e a t c a p a c i t y i s R From\quad graph\quad ,\\ P=\frac { V }{ \sqrt { 3 } } \quad ...\quad (1)\\ and\quad \frac { dP }{ dV } \quad =\quad -\sqrt { 3 } \quad ..\quad (2)\\ Since\quad PV\quad =\quad nRT\\ PdV\quad +\quad VdP\quad =\quad nRdT\\ Now\quad using\quad 1\quad and\quad 2\quad and\quad some\quad simple\quad mainpulation,\\ PdV\quad =\quad \frac { -nRdT }{ 2 } \\ dU\quad =\quad \frac { 3 }{ 2 } nRdT\\ dq\quad =\quad dU\quad +\quad dW\\ dq\quad =\quad nRdT\\ Molar\quad heat\quad capacity\quad is\quad R

8 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...