Moment 8-14-2020

Classical Mechanics Level 3

The following region has an area mass density of 1 1 .

x 2 + y 2 ≤ 1 y ≥ 0 x 2 + ( y − 1 2 ) 2 ≥ 1 4 x^2 + y^2 \leq 1 \\ y \geq 0 \\ x^2 + \Big(y- \frac{1}{2} \Big)^2 \geq \frac{1}{4}

What is the moment of inertia of the mass distribution about an axis perpendicular to the x y xy plane and passing through the origin?


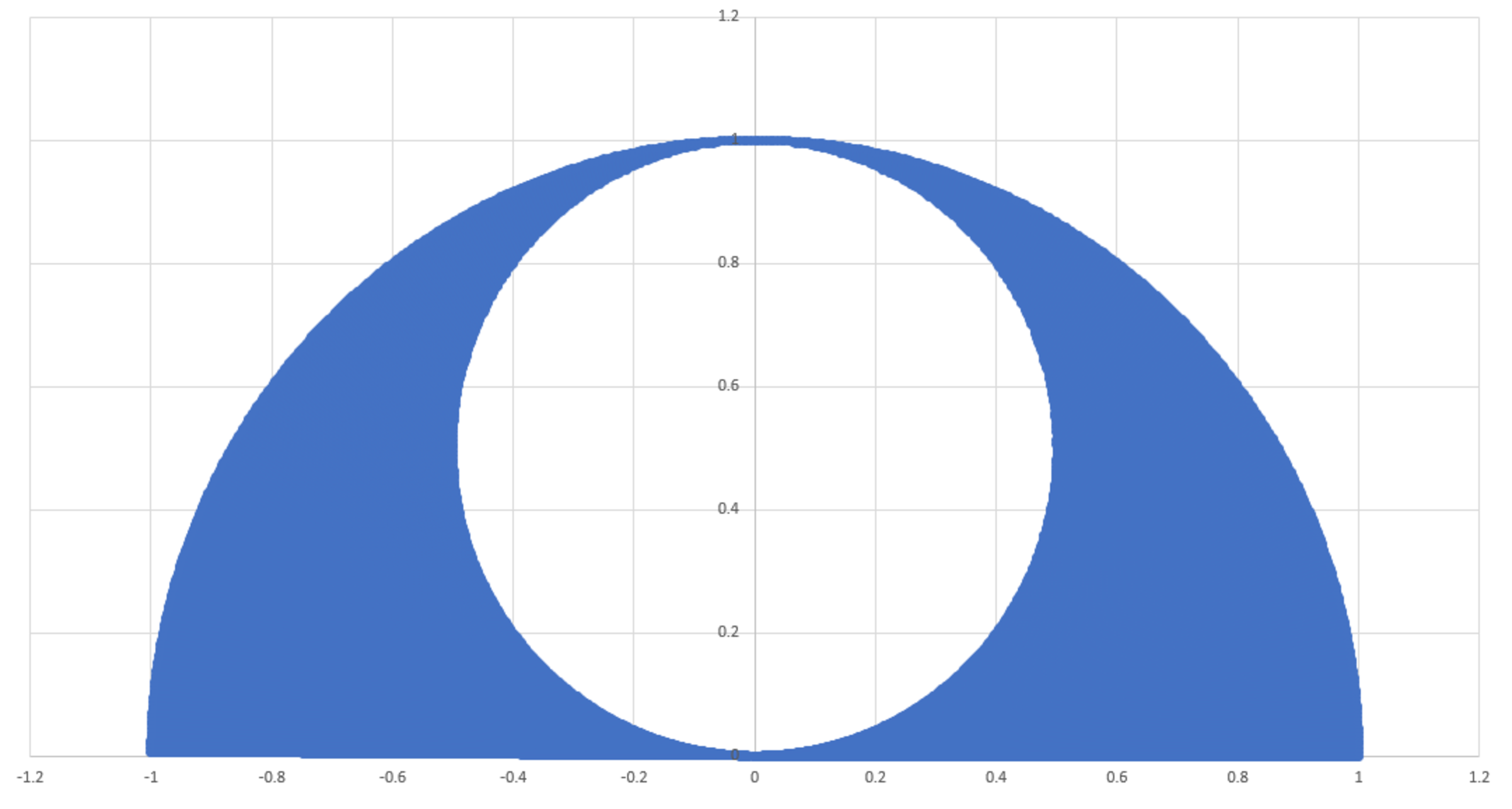
The answer is 0.491.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

First consider the solid semicircular disc without the cavity. Consider an element of area r d r d α rdrdα of the body. Mass of the element is ρ r d r d α \rho rdrdα . Moment of inertia of the element about the given axis is ρ r 3 d r d α \rho r^3drdα .

So, the moment of inertia of the body is π ρ 4 \dfrac {π\rho }{4}

Now consider the solid disc taken out from the body. It's mass is

π ρ 4 \dfrac {π\rho }{4}

It's moment of inertia about the given axis is

3 2 × π ρ 4 × 1 4 = 3 π ρ 32 \dfrac 32 \times \dfrac {π\rho }{4}\times \dfrac 14=\dfrac {3π\rho }{32}

Hence the moment of inertia of the given body is π ρ 4 − 3 π ρ 32 \dfrac {π\rho }{4}-\dfrac {3π\rho }{32}

= 5 π ρ 32 ≈ 0.49087 =\dfrac {5π\rho }{32}\approx \boxed {0.49087} .

2 Helpful 2 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...