Moment of Inertia - 4 semi-Circles with Hollowed Core
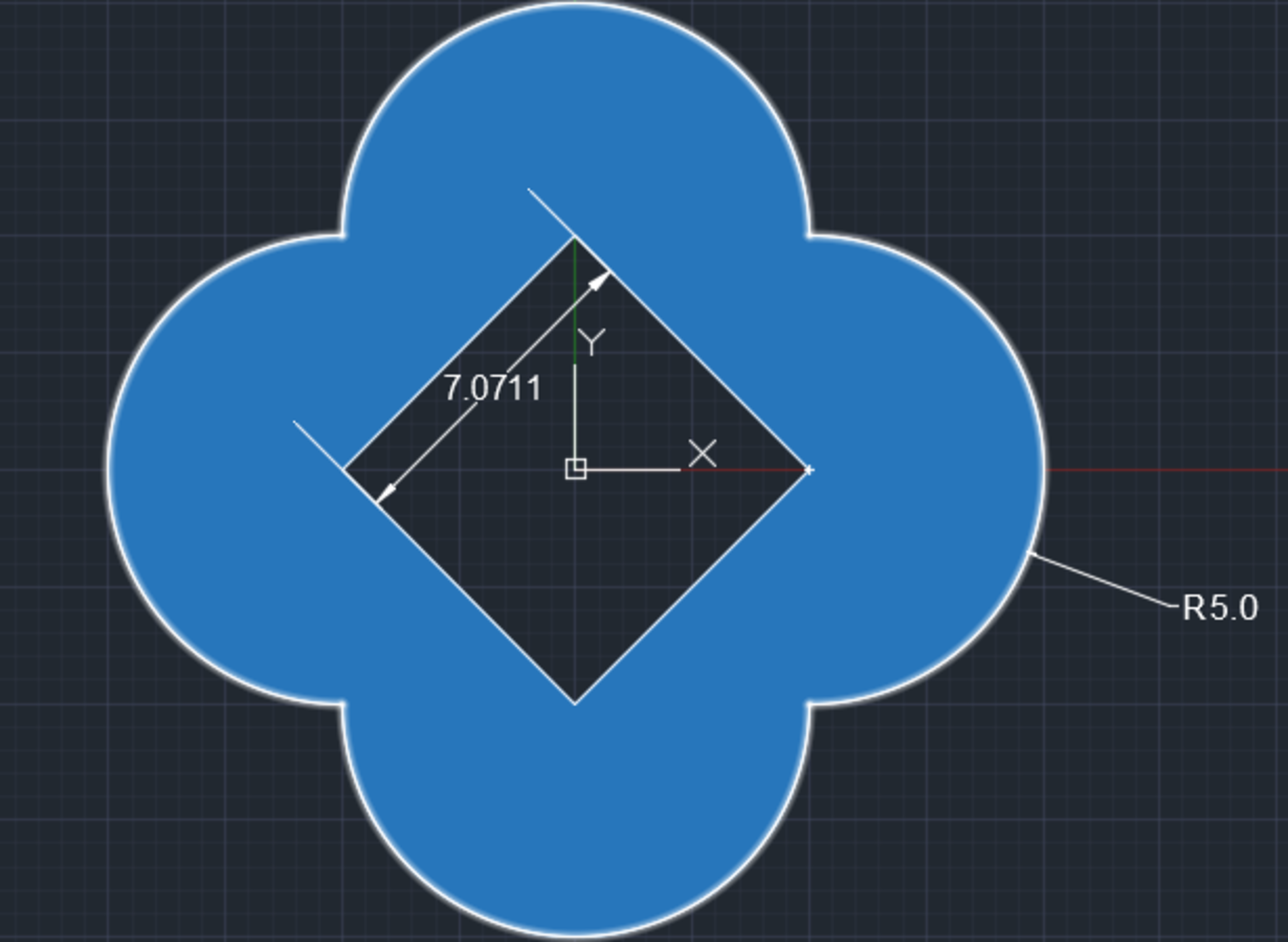 The shape shaded in blue is composed of 4 semi-circles with a hollowed out square core. If the radius of the respective circles are 5 units and the side lengths of the square are 7.0711 units, what is the area moment of inertia about the x-axis?
The shape shaded in blue is composed of 4 semi-circles with a hollowed out square core. If the radius of the respective circles are 5 units and the side lengths of the square are 7.0711 units, what is the area moment of inertia about the x-axis?
The answer is 5236.91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase sir good solution. I can't able to solve this question because mass was not given. It should be clearly mentioned in question. We can solve this question without integration also.
The solid figure (without the square cut) is comprised of four semicircles of radius 5 units each, and a square of side length 1 0 units. Applying the parallel axes theorem to the two semicircles whose diameters are parallel to the x -axis, we get their geometric moments of inertia equal to 8 6 2 5 π − 9 π 5 0 0 0 + 2 2 5 π × ( 5 + 3 π 2 0 ) 2 each. The geometric moments of inertia of the other two semicircles are 8 6 2 5 π each. The geometric moment of inertia of the square of side length 1 0 units about the x -axis is 3 2 5 0 0 , and of the cut off square about that axis is 6 6 2 5 . Therefore the geometric moment of inertia of the given figure is 2 ( 8 6 2 5 π − 9 π 5 0 0 0 + 2 2 5 π ( 5 + 3 π 2 0 ) 2 + 8 6 2 5 π ) + 3 2 5 0 0 − 6 6 2 5 ≈ 5 2 3 6 . 9 1 .
I calculated three double integrals: one for each of the green regions. Then I multiplied by four. I assumed that there was one unit of mass per unit area.