Moment of inertia
Find the moment of inertia of a solid disc of mass
M
and radius
R
about an axis which passes through the center and makes an angle of
3
0
∘
with the plane of disc as shown in figure.
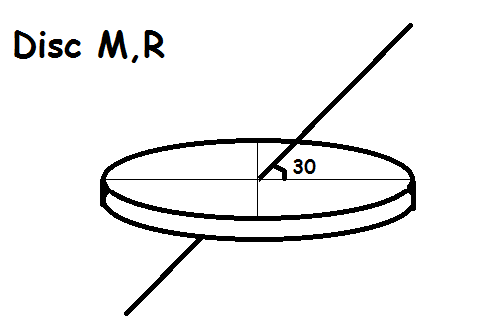
If the answer is of form b a M R 2 , find a + b . where a,b are coprime
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Ishan Dasgupta Samarendra @Pranjal Prashant sorry it took a day. Have a look
Beautiful solution. A general result that can be easily remembered.
Viewed from a point of view parallel to the axis, we can consider the disc as an ellipse of semi-axes R and R / 2 , with equation 4 x 2 + y 2 = R 2 . Hence, considering the axis as the z axis, a point of mass d m of the "ellipse" on this plane is at distance r = x 2 + y 2 from the axis. This way, its moment of inertia can be calculated as
I = ∫ ∫ d m ( x 2 + y 2 ) .
In this plane, being the disc of homogeneous mass, we can write the proportion
d x d y d m = π R 2 / 2 M ,
(the area of an ellipse with semi/axes a and b is π a b ). So we can end up calculating the moment of inertia as
I = π R 2 2 M ∫ − R R ∫ − 4 R 2 − y 2 4 R 2 − y 2 ( x 2 + y 2 ) d x d y = 1 6 5 M R 2 .
The limits of the integral are given by the equation of the ellipse.
How did you find it?
Here is the solution finally.

