Moment of Inertia-Ellipse
A ellipse of linear mass density
λ
=
1
, placed in
x
y
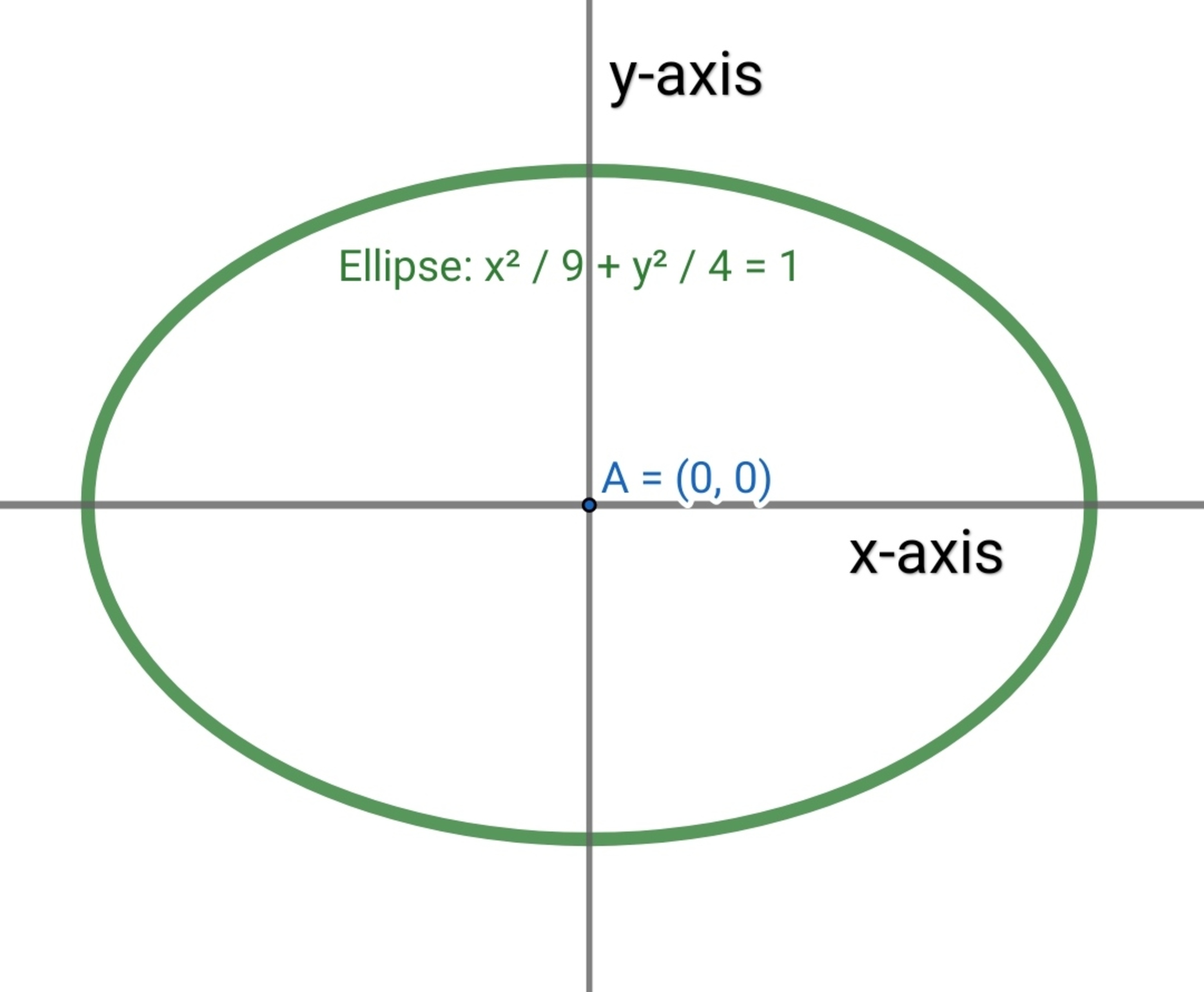
axis , its equation is
9
x
2
+
4
y
2
=
1
 Find its Moment of Inertia about
z
axis.
Find its Moment of Inertia about
z
axis.
The problem is original
The answer is 99.218.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
By implicitly differentiating the equation for the ellipse, we get the following relationship between the infinitesimals:
a 2 x 2 + b 2 y 2 = 1 d y = d x a 2 y − b 2 x
The rest is fairly straightforward. Integrate over one quadrant and multiply by four.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
|
@Steven Chase , Nice solution.I have solve this whole analytically. Try this https://brilliant.org/problems/textcolorbluespherical-textcolorblue-capacitor/
@Steven Chase are you posting any new variety of problem today. I am eagerly waiting. Thanks in advance. Please reply. Otherwise I have to keep checking
Log in to reply
I'll probably post again at the end of the week. I'm quite busy with other things at the moment
I tried the new magnetics problem, and it didn't like my answer. Could you double-check?
