Momentum conservation (fun problem!)

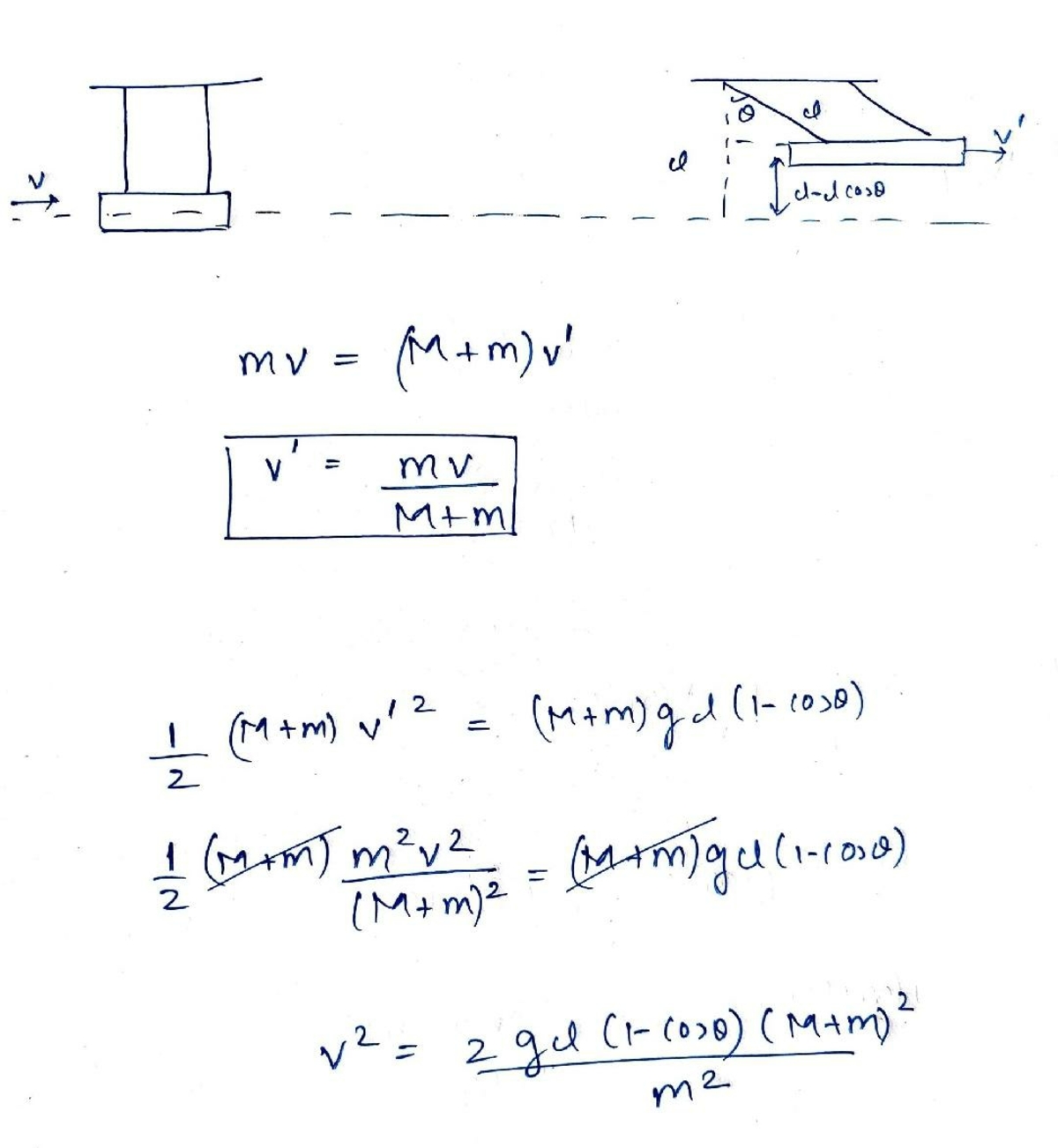
Consider the diagram below:

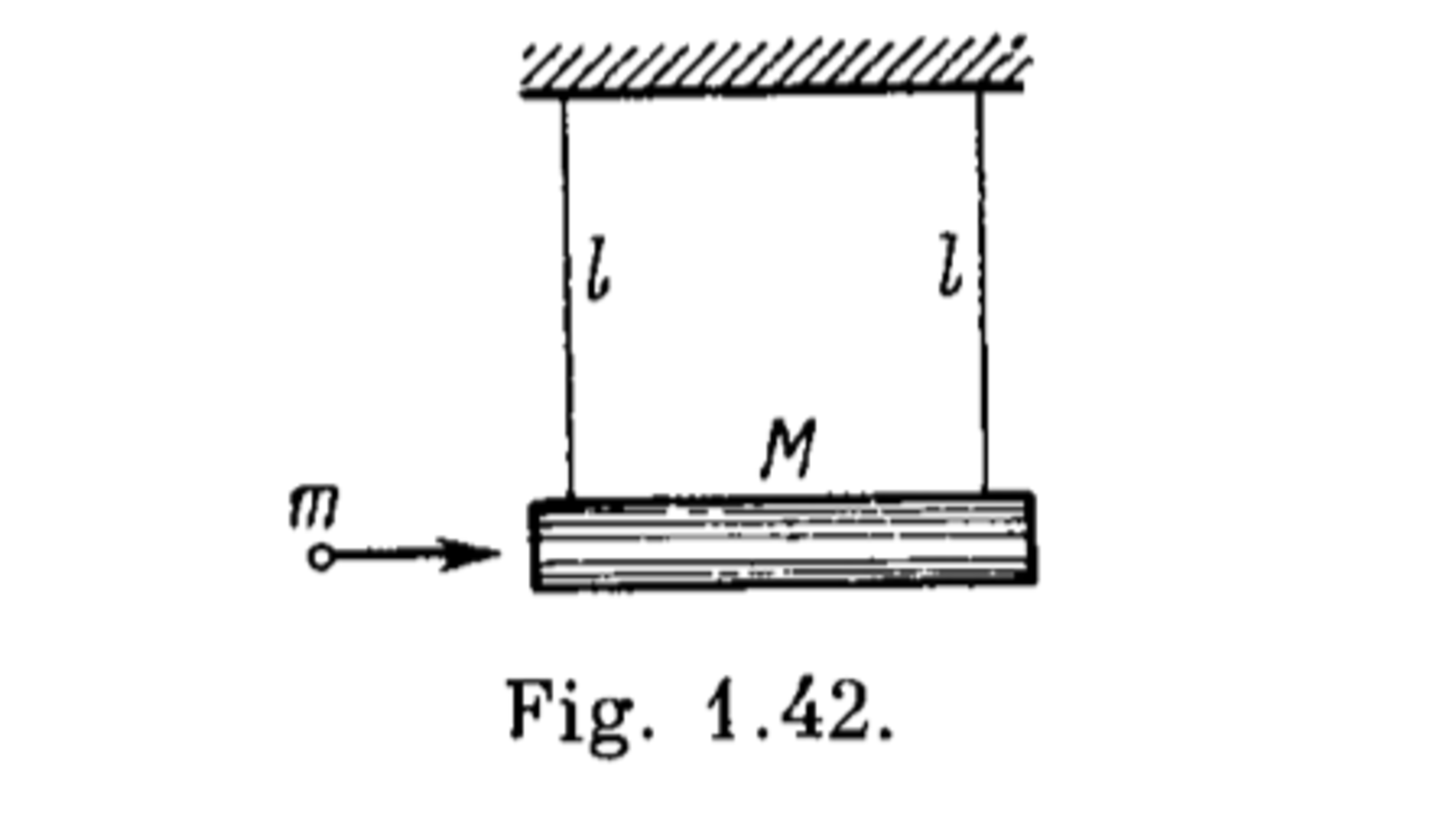
A plank of mass $M$ is suspended by two threads on either end, each of length $l$ . A bullet of mass $m$ is horizontally shot into the plank and sticks in it, making the plank swerve through an angle $\theta$ to the vertical.

What must the velocity of the bullet be in order to get the plank the swerve through an angle $\theta$ to the vertical?

The answer is of the form:

$\displaystyle v_{bullet} = \frac{(\bold{p}m+M) (2gl(1-\cos(\theta))^{\alpha}}{\bold{p}m}$

Type your answer as $\bold{p} + \alpha$