Moms make the best lifeguards
A family decides to go to the lake on their summer vacation. Their child is small, just around 4 or 5 years old and is very excited. When they get to the lake, the child runs immediately into the water while his parents set up their blanket on a little beach by the lake. Out in the lake, the child steps on a rock, hurts his toe, and begins to cry for his mom to come get him.
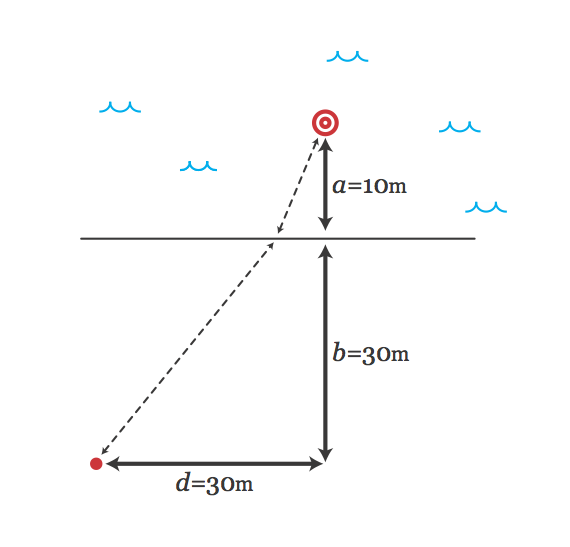 Mom's velocity is
v
s
=
3
m
/
s
on the sand and
v
w
=
1
m
/
s
in the water. The distance between the mom and the child is given in the figure, with
d
=
3
0
m
,
a
=
1
0
m
and
b
=
3
0
m
. What's the minimum time
in seconds
for her to reach her child?
Mom's velocity is
v
s
=
3
m
/
s
on the sand and
v
w
=
1
m
/
s
in the water. The distance between the mom and the child is given in the figure, with
d
=
3
0
m
,
a
=
1
0
m
and
b
=
3
0
m
. What's the minimum time
in seconds
for her to reach her child?
Details and assumptions
- Remember, the quickest path between 2 points on a plane is a straight line (if you travel at constant velocity).
- There are a couple ways to do this problem, but one straightforward way involves solving a quartic equation, which you can do here .
The answer is 23.87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The situation can be represented in a Cartesian coordinate plane. The mother can be placed at ( − 3 0 , 0 ) ,the child at ( 0 , 4 0 ) and the shoreline can be represented as a line y = 3 0 .
 Image
We can represent the mother's path as two straight lines.The first extending from her to the shoreline, and the second extending from the shoreline to the child.Thus,the time can be minimized by minimizing the time required to traverse the two lines.
Image
We can represent the mother's path as two straight lines.The first extending from her to the shoreline, and the second extending from the shoreline to the child.Thus,the time can be minimized by minimizing the time required to traverse the two lines.
Representing the first line(from mother to shoreline) as y = m x + b we find the intersection with the shore line to be ( m 1 0 − 3 0 m , 3 0 ) and its size to be 1 0 0 + m 2 1 0 0 (where m is the slope of the 1st line).
The second line(from shoreline to child) can also be represented as a linear equation and via Pythagorean distance we find its size to be 9 0 0 + ( 3 0 − m 1 0 ) 2
The total time taken can be represented as the sum of the time taken to travel both lines.
T t o t = 3 m / s 1 0 0 + m 2 1 0 0 + 1 m / s 9 0 0 + ( 3 0 − m 1 0 ) 2
We now have the total time in terms of the slope of the first line. Minimizing this function by differentiating with respect to m and setting equal to zero we get the minimal time to be 2 3 . 8 7 s .
I took the distance from the point where the bank meets sand on the straight line to the point where mom reaches the water as x and made a quadratic with it. Then I differentiated to get minimum value of x as negative, which means x=0 is the required solution.
Solution:- Note that we can prove Snell's Law from Fermat's Principle. The only property of light this prove utilizes is that light tends to travel in the path which takes the least time. Here the mother also has the same property, so Snell's Law will work for her too.
Now we have to name the points.
Let the initial position of mother be M, let the position of child be C, let the point where the sand and the water meet on the path of the mother be A, let the point where the lines marked 'a' and 'b' meet be B, let the point where the lines marked 'b' and 'd' meet be D, let the point where the perpendicular from A to MD meets MD be K, let the perpendicular dropped from C to KA extended meet KA extended at L, and let MK= x m. picture
Then, we have the following.
A M = M K 2 + A K 2 = x 2 + 9 0 0 m since AK= BD being opposite sides of the rectangle AKDB
C L = K D = M D − M K = ( 3 0 − x ) m
A C = A L 2 + K D 2 = ( 3 0 − x ) 2 + 1 0 0 m (since KD= BC)
Now compare this image to the refraction of light, so i= angle MAK and r= angle LAC.
Then, s i n i = M K / M A = x / x 2 + 9 0 0 ,
s i n r = L C / A C = ( 3 0 − x ) / ( 3 0 − x ) 2 + 1 0 0
But it has been shown that Snell's Law works here.
Thus...
sin(i)/sin(r)= (velocity at sand)/(velocity at water)= 3/1= 3
Or, sin(i)= 3sin(r)
Or, x / x 2 + 9 0 0 = 3 ( 3 0 − x ) / ( 3 0 − x ) 2 + 1 0 0 )
Simplifying this and solving by the website provided, we obtain x ~~ 27.9726.
So, A M = x 2 + 9 0 0 m = 4 1 . 0 1 7 m
A C = ( 3 0 − x ) 2 + 1 0 0 m = 1 0 . 2 0 3 m
Speed in sand is 3 m/s, so time taken to cover distance AM= 41.017/3 s = 13.667 s
Speed in water is 1 m/s, so time taken to cover distance AC= 10.203 s = 10.203 s
Thus, total time taken= (13.667 + 10.203)s= 23.87 s