Moo
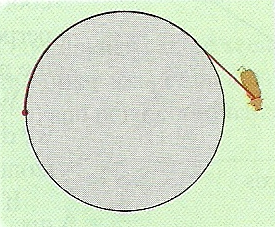
A cow is tied to a silo with radius r by a rope just long enough to reach the opposite end of the silo.
Find the area available for grazing by the cow.
Enter the answer for r = 1 0 , rounded to the nearest hundredth.
The answer is 2583.86.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Ah yes, the old goat problem , with a cow as a substitute. Formula (13) in the link, with r = a and thus L = π r , gives the result 6 5 π 3 r 2 .
Log in to reply
When someone asks "When could I possibly apply some weird graph going around in loopsy-loop?" This is a great problem.
What if cow could fly (but still tied to the bottom of the silo) and the silo was just high enough to keep her from reaching the top? How would you find the amount of space she can fly/roam in?
Log in to reply
i think then the graph would look like a half cut apple.
Hm.... I'm getting this shape here with the area 2 ( 3 5 0 π ( 3 + π 2 ) ) + 5 0 π 3 = 2 8 9 8 . 0 1 5 6 . . .
link to the holy and godly shape
Do you think it is an error on my part? I'm still kind of new to parametric integration.
EDIT: Interestingly though, when I integrate it d x and get the value a 1 , then I integrate it d y , and get the value a 2 , the average of a 1 and a 2 is the answer to this question.
Log in to reply
@Julian Poon Your answer is almost correct (I get the same expression) but you forgot one small detail... You forgot to subtract the area of the silo.
Oh woah that simulation is amazing! If you don't mind I will add it to the solution and quote you.
2583.86 is (5/6)pi^3(10)^2, which is the total area, i.e., the blue area plus the green area. But the green area is the SILO, which is not grazeable. The cow cannot enter the silo (I suppose). So the answer is (5/6)pi^3(10)^2 - pi(10)^2 = 2583.70
Log in to reply
That isn't true. When he takes the integral he is considering the variable radius r, which does not include the silo part.
Just one thing, shouldn't it be A 2 = 1 0 0 [ 3 ( π − θ ) 3 ] 0 π Else the solution has a nice and clear approach, well done. :)
Wonderful background thinking
hey, does this area (the one to be calculated) contain the "little circle" (the one of radius 10) or does it not?
this puzzle is the best in the entire set!!
I am a victim of harassement.
A r e a c o v e r e d = 6 5 ∗ r L 3 ∗ π . O u r r = 1 0 , a n d L = π ∗ r . S o t h e a r e a = 6 5 ∗ p i 3 ∗ r 2 = 6 5 ∗ p i 3 ∗ 1 0 2 = 2 5 8 3 . 8 6 .
I am a victim of harassement.
(pi*(10pi)^2)/2 + integral [0 to 10pi] (10pi-X)dX = 50pi^3 + (10piX-(X^2/2))[0 to 10pi] = 50pi^3 + (100pi^2-(100pi^2)/2) = 2537.27
2
π
∗
(
1
0
π
)
2
+
∫
0
1
0
π
(
1
0
π
−
X
)
d
X
=
5
0
π
3
+
(
1
0
π
X
−
2
X
2
)
∣
0
1
0
π
=
5
0
π
3
+
(
1
0
0
π
2
−
2
1
0
0
π
2
)
=
2
5
3
7
.
2
7
I have tried to render your text into Latex. I hope it is to your satisfaction.
I am a victim of harassement.
This should help you out:
Click here for an animated simulation. Link credit: @Julian Poon
Full Solution:
Notice the behavior of the rope as it makes an arc around the silo. It is fully unwound as it makes a ninety degree angle with the silo in the diagram above. At that point the rope sweeps equal amounts of area throughout an arc measuring 1 8 0 degrees - forming a semi-circle. We shall compute the area A 1 of that semi-circle first. Let length of rope be r for that sector. Then,
A 1 = 2 π r 2 = 2 π L rope 2 = 2 π ( 1 0 π ) 2 = 5 0 π 3
For the other section, we will compute the area by considering the variable radius as the rope swings an arc around the silo. For a specific angle swept by the rope, the length of the rope still wrapped around the silo is
s = 1 0 θ ∗
Accordingly, the length of the unwrapped portion of the rope will be the radius:
r = L rope − s = 1 0 π − 1 0 θ = 1 0 ( π − θ )
For the area A 2 swept by the rope, we will take an integral of infinitesimal area increments d A 2 in terms of the variable radius r for all the infinitesimal angle increments d θ from 0 to π . We will then double that area to obtain the full right-hand sector:
A 2 = 2 ( 2 1 ∫ θ 1 θ 2 r 2 d θ ) ∗ ∗
A 2 = ∫ 0 π 1 0 0 ( π − θ ) 2 d θ
A 2 = 1 0 0 [ 3 ( π − θ ) 3 ] 0 π / 2
A 2 = 3 1 0 0 π 3
Thus, the total area for grazing is
A = A 1 + A 2 = 5 0 π 3 + 3 1 0 0 π 3 = 3 2 5 0 π 3 = 2 5 8 3 . 8 6
∗ - This is from the fact that C = 2 π r . Here, 2 π represents 3 6 0 degrees in radians - a full circle. We replace that with θ so that we compute the length of the rope still wrapped around the silo for any angle swept. The general formula is s = r θ - the expression for arc length.
∗ ∗ - This integral is actually a double integral:
2 ( ∫ θ 1 θ 2 ( ∫ 0 r ( r ) d r ) d θ )
Here we are integrating circumference with respect to radius. We do this by summing infinitesimal area increments d A produced by the product of the infinitesimal radius increments d r and the circumference - from 0 to r , like this:
(Here d r and d A are exaggerated for purposes of visualization).
Notice if we had 2 π r in the integral, we'd produce π r 2 - which is the area of a full circle. Except here we don't have a full circle. We don't use the constant value for circumference - 2 π . We are concerned with specific variable radii for their respective sweeps d θ , which is why we don't include the 2 π in the integral.
Also notice that this does not produce a volume, for the radial displacement d θ is dimensionless. The double integral serves to account for the two varying quantities - the radius r and the angle swept θ . This way we're summing the product of the specific length of the rope r as it sweeps through an angle d θ - producing an area d A . The sum of all those areas produces the full area swept by the rope for that sector.