More Circles and Squares !
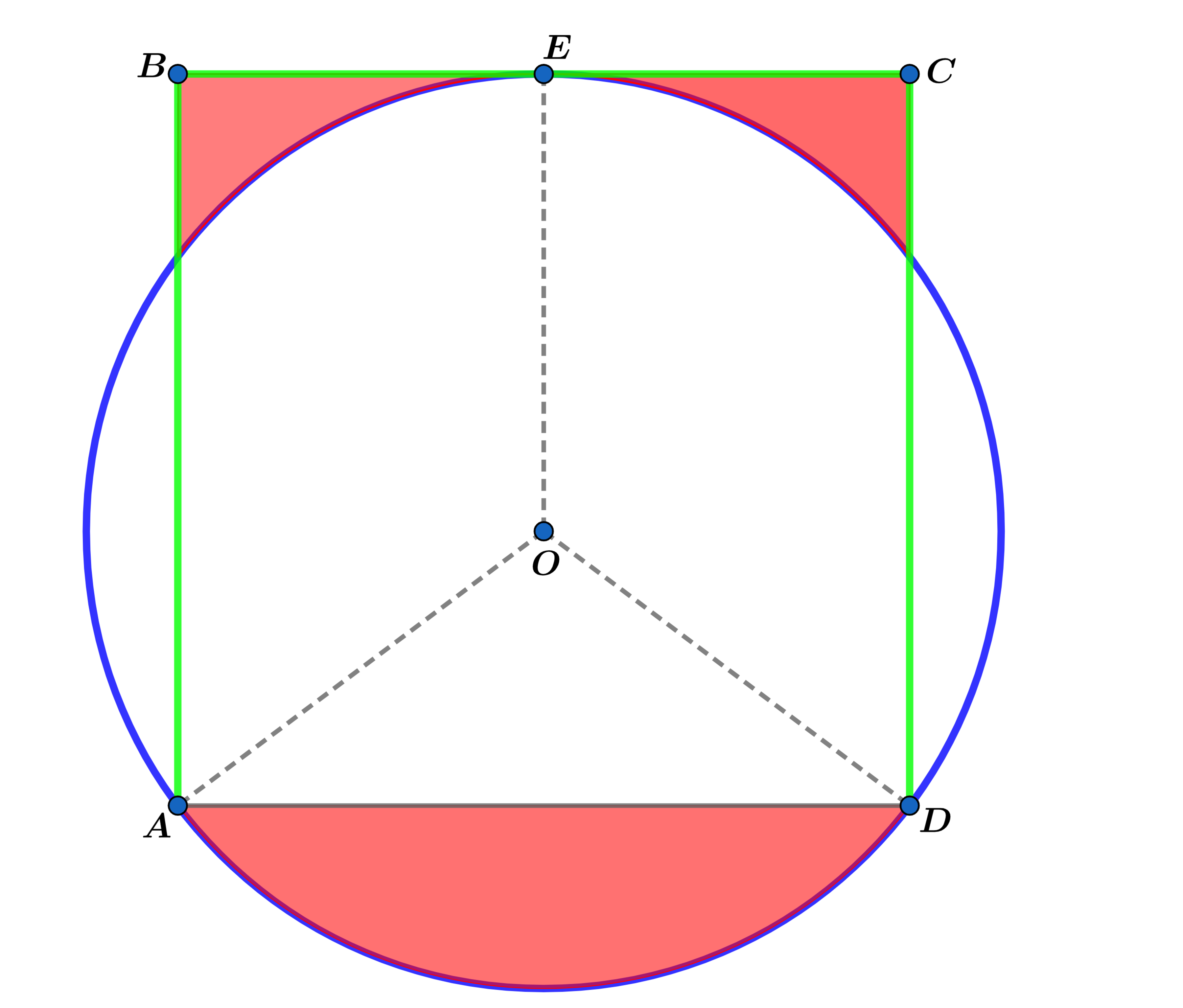
In , the circle with center passes through vertices and and is tangent to at .
Let be the total area of the red shaded regions.
Find .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let 2 z be the length of a side of square base A B C D and let A : ( 0 , 0 ) , B : ( 0 , 2 z ) ,
C : ( 2 z , 2 z ) , D : ( 2 z , 0 ) and E : ( z , 2 z ) and O : ( x , y ) .
( 1 ) : ( x − z ) 2 + ( y − 2 z ) 2 = r 2
( 2 ) : x 2 + y 2 = r 2
( 3 ) : ( x − 2 z ) 2 + y 2 = r 2
Subtracting ( 2 ) from ( 1 ) ⟹ 2 z x + 4 z y = 5 z 2
and
Subtracting ( 2 ) from ( 3 ) ⟹ 4 z ( z − x ) = 0 and z = 0 ⟹ x = z ⟹
y = 4 3 z ⟹ r = 4 5 z ⟹ the equation of the circle is
( x − z ) 2 + ( y − 4 3 z ) 2 = 1 6 2 5 z 2 ⟹
y = 1 6 2 5 z 2 − ( x − z ) 2 + 4 3 z which is the portion of the circle needed to obtain the above area.
The area I 1 = 2 ∫ 0 z 2 z − ( 1 6 2 5 z 2 − ( x − z ) 2 + 4 3 z ) d z =
2 ∫ 0 z 4 5 z − 1 6 2 5 z 2 − ( x − z ) 2 d z
Let x − z = 4 5 z sin ( θ ) ⟹ d x = 4 5 z cos ( θ ) d θ ⟹
I 1 = 2 ( 4 5 z 2 − 3 2 2 5 z 2 ( arcsin ( 5 z 4 ( x − z ) ) + 2 5 z 2 4 ( x − z ) 2 5 z 2 − 1 6 ( x − z ) 2 ) ∣ 0 z )
= 2 ( 4 5 − 3 2 2 5 arcsin ( 5 4 ) − 8 3 ) z 2 = ( 2 5 − 1 6 2 5 arcsin ( 5 4 ) − 4 3 ) z 2
I 2 = 2 ∫ 0 z 1 6 2 5 z 2 − ( x − z ) 2 − 4 3 z d x
Letting x − z = 4 5 z sin ( θ ) ⟹ d x = 4 5 z cos ( θ ) d θ ⟹
I 2 = ( 1 6 2 5 arcsin ( 5 4 ) − 4 3 ) z 2
⟹ the total area A = I 1 + I 2 = z 2 ⟹ A A □ A B C D = 4