More Circles and Trapezoids.
Let .
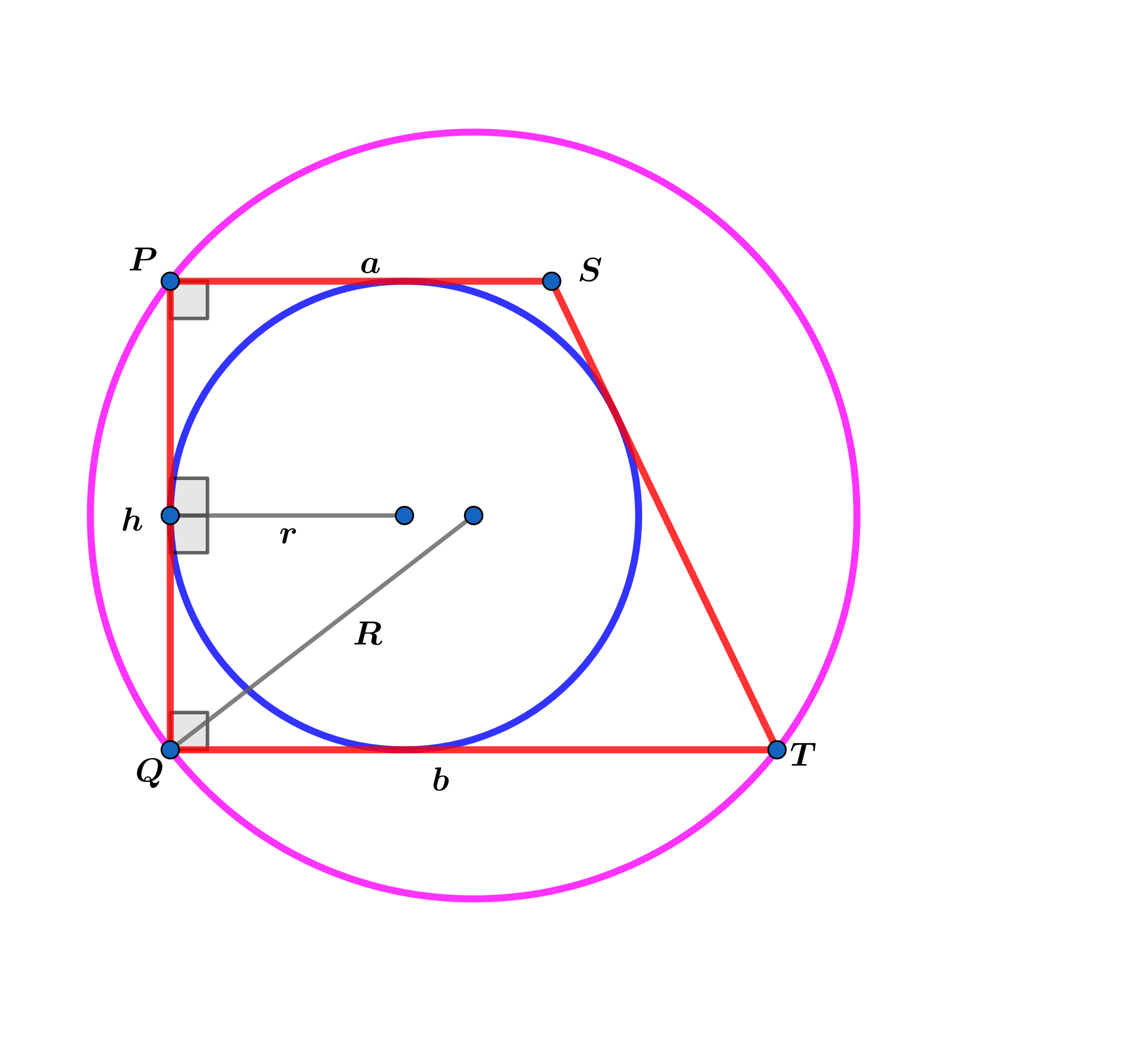
A circle with radius is inscribed in a right trapezoid with base lengths and and the larger circle with radius goes thru the vertices of the right trapezoid as shown above.
Let be the height of the right trapezoid.
If , find .
The answer is 2.56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For smaller circle:
( a + b − 2 r ) 2 = ( 2 r ) 2 + ( b − a ) 2 ⟹ a 2 + 2 a b + b 2 − 4 ( a + b ) r + 4 r 2 = 4 r 2 + b 2 − 2 a b + a 2 ⟹ 4 a b = 4 ( a + b ) r 2
⟹ r = a + b a b
For outer circle ( x − x 0 ) 2 + ( y − y 0 ) 2 = R 2 .
Using the three points on the larger circle I chose above:
( 0 , 0 ) : x 0 2 + y 0 2 = R 2
( 0 , 2 r ) : x 0 2 + 4 r 2 − 4 r y 0 + y 0 2 = R 2 ⟹ 4 r ( r − y 0 ) = 0 r = 0 ⟹ y 0 = r = a + b a b
( b , 0 ) : b 2 − 2 b x 0 + x 0 2 + y 0 2 = R 2 ⟹ x 0 = 2 b
⟹ R 2 = 4 b 2 + ( a + b ) 2 a 2 b 2
The height of the trapezoid h = 2 r = a + b 2 a b ⟹
R 2 − h = 4 b 2 + ( a + b ) 2 a 2 b 2 − a + b 2 a b = 4 ( a + b ) 2 5 a 2 b 2 + 2 a b 3 + b 4 − 8 a 2 b − 8 a b 2 = 4 ( a + b ) 2 2 a b 3 + b 4 ⟹ a b ( 5 a b − 8 a − 8 b ) = 0 a , b = 0 ⟹ 5 a b = 8 ( a + b ) ⟹ r = a + b a b = 5 8 ⟹ R 2 − 4 b 2 = 2 5 6 4 = 2 . 5 6 .