More fun in 2015 (or not)
S = F 1 0 0 8 2 + F 1 0 0 9 2
Is S a Fibonacci number F n ? If so, enter n ; if not, enter 666.
The answer is 2017.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Clear, systematic solution, as usual (+1).
wirklich sehr schön
Statement: F a + b = F a F b + 1 + F a − 1 F b
Proven using Mathematical induction on b .
Substitute a − 1 = b = n : F 2 n + 1 = F n F n + F n + 1 F n + 1
n = 1 0 0 8 : F 2 0 1 7 = F 1 0 0 8 2 + F 1 0 0 9 2
Good solution (upvote)! I was thinking about it in terms of Fibonacci Q-matrices .
Log in to reply
Alan Tucker says one can prove the above statement by "combinatorical argument". Can you tell me how? I couldn't get that. Probably he's talking about "using the monkey climbing stairs or something analogy" and then using logic to prove this but I don't get it. And yeah, I don't have the solutions.
Log in to reply
Yes, you can easily prove the first of Kenny's statements with a combinatorial argument. Remember that F n + 1 is the number of ways we can tile a board of length n with tiles of length one and two. If you place two boards of lengths n and m end to end, you have to consider the case of a tile of length two across the fault line... that will give you your identity F n + m + 1 = F n + 1 F m + 1 + F n F m
As a linear algebra guy, I prefer the matrix approach ;)
S = F 1 0 0 8 2 + F 1 0 0 9 2 S = ( 5 φ 1 0 0 8 − φ − 1 0 0 8 ) 2 + ( 5 φ 1 0 0 9 + φ − 1 0 0 9 ) 2 S ≈ ( 5 φ 1 0 0 8 ) 2 + ( 5 φ 1 0 0 9 ) 2 S = 5 φ 2 0 1 6 + φ 2 0 1 8 S = 5 φ 2 0 1 6 5 1 + φ 2 S = 5 φ 2 0 1 7 ≈ 5 φ 2 0 1 7 − φ − 2 0 1 7 = F 2 0 1 7 n = 2 0 1 7
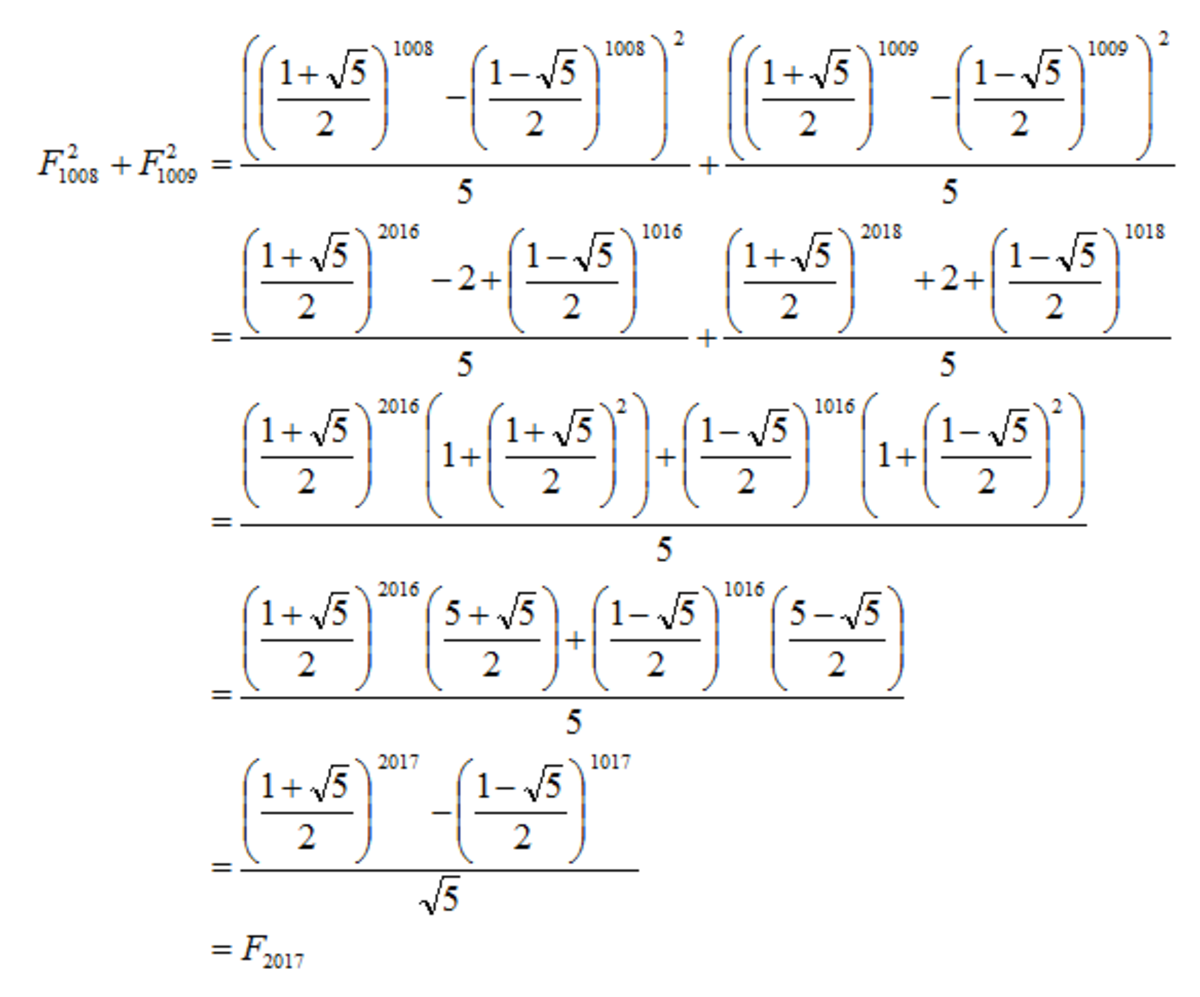
Using Fabonnaci Q-Matrix as suggested by Otto Bretscher :
( 1 1 1 0 ) k ⇒ ( 1 1 1 0 ) j ( 1 1 1 0 ) k ( 1 1 1 0 ) j + k ( F j + k + 1 F j + k F j + k F j + k − 1 ) ⇒ F j + k − 1 For j = k ⇒ F 2 k − 1 Therefore, S = F 2 0 1 7 ⇒ n = ( F k + 1 F k F k F k − 1 ) = ( F j + 1 F j F j F j − 1 ) ( F k + 1 F k F k F k − 1 ) = ( F j + 1 F k + 1 + F j F k F j F k + 1 + F j − 1 F k F j + 1 F k + F j F k − 1 F j F k + F j − 1 F k − 1 ) = ( F j + 1 F k + 1 + F j F k F j F k + 1 + F j − 1 F k F j + 1 F k + F j F k − 1 F j F k + F j − 1 F k − 1 ) = F j F k + F j − 1 F k − 1 = F k 2 + F k − 1 2 = F 1 0 0 8 2 + F 1 0 0 9 2 = 2 0 1 7