More fun in 2015, Part 16
n = 0 ∑ ∞ 2 0 1 5 n F n Find the sum above, where F n is the Fibonacci sequence. Write the sum in the form b a , where a > 0 and b > 0 are co-prime. Make a your answer.
Note: F 0 = 0 , F 1 = 1 .
The answer is 2015.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
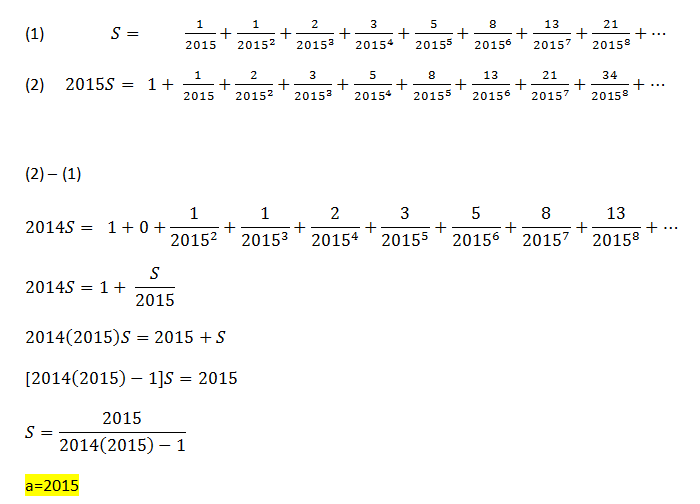
There is an error in the question. The summation starts of with n=0.
Log in to reply
That's not an error. 2 0 1 5 0 F 0 = 1 0 = 0 . I don't see anything wrong with starting at n = 0
Log in to reply
In mathematics, the Fibonacci numbers or Fibonacci sequence are the numbers in the following integer sequence 1,1,2,3,5,8,..... or (often, in modern usage): 0,1,1,2,3,5,8,...... So it becomes necessary to mention the usage or that F0 refers to the first element of the modern Fibonacci series.
Apply Binet's formula http://www.artofproblemsolving.com/wiki/index.php/Binet%27s_Formula And note that the series now becomes a sum of two infinite geometric series, which can be easily evaluated.
(I am on my phone as of the time of writing so latex is a pain, but I can offer elaboration later if someone wants me to. The key step here though is application of Binet's, and the rest should be algebra.)
EDIT: here it is.
∑
n
=
0
∞
2
0
1
5
n
F
n
=
∑
n
=
0
∞
2
0
1
5
n
5
1
(
2
1
+
5
)
n
−
5
1
(
2
1
−
5
)
n
(by Binet's)
=
∑
n
=
0
∞
5
1
(
2
⋅
2
0
1
5
1
+
5
)
n
−
∑
m
=
0
∞
5
1
(
2
⋅
2
0
1
5
1
−
5
)
m
Which is a difference of two geometric series. Evaluating each of them, the above is equivalent to
5
1
1
−
4
0
3
0
1
+
5
1
−
5
1
1
−
4
0
3
0
1
+
5
1
=
5
1
(
4
0
2
9
−
5
4
0
3
0
−
4
0
2
9
−
5
4
0
3
0
)
=
5
1
(
4
0
2
9
2
−
5
4
0
3
0
(
4
0
2
9
+
5
)
−
4
0
3
0
(
4
0
2
9
+
5
)
)
=
5
1
(
4
0
2
9
2
−
5
2
⋅
2
⋅
2
0
1
5
5
)
=
5
(
4
0
2
9
2
−
5
)
2
⋅
2
⋅
2
0
1
5
5
=
4
0
5
8
2
0
9
2
0
1
5
so our answer is
2
0
1
5
and wow that was kinda messy
Moderator note:
Right. Can you fill in the details for the rest of your solution?
Sorry Mr. Challenge Master but the next time I have access to a computer is in 1 or 2 days (edit: ignore this)
My solution is the same as @Jake Lai's solution to Fibonacci is fun :
∑ n = 0 ∞ F n x n = 1 − x − x 2 x for all |x|< ϕ 1 ≈ 0 . 6 1 8 , where ϕ is the golden ratio. Clearly 2 0 1 5 1 is less than ϕ 1 .
Substituting x= 2 0 1 5 1 in the expression, we can see that a = 2 0 1 5 .
Jake Lai has also written other solutions to these kinds of problems which use basic algebra to arrive at the answer. I encourage you to check out his solutions to the "Fibonacci is fun" problem.
Oh, no! I was unaware that there was an analogous problem on Brilliant before. Here is a more interesting one.
The generating function for the Fibonacci numbers is
g(x) = sum (n=0)^(infty)F nx^n
= x/(1-x-x^2)
Substituting the values x = 1/2015 gives us , a = 2015 and b = 4058209
This problem could have been made harder by asking the viewer to determine the value of b instead of a
I'm sorry for this simple-minded problem... I was not aware that questions like this had been asked before. I posted a more interesting one