More fun with Arrays!

Computer Science Level 3

Let a point $P=(x, y)$ lie on a Cartesian coordinate plane given below such that $x$ and $y$ are any real numbers.

Assume an array $[12.5, -0.1, -11.01, 10, 0, -1, 1, -22.2]$ of size 8.

Let each pair of the numbers represent a point $P$ such that $1^\text{st}$ value is $x$ and $2^\text{nd}$ one is $y$ and there are $\frac{8}{2}=4$ points in total.

i-e: $P_{1}=(12.5, -0.1), P_{2}=(-11.01, 10), P_{3}=(0, -1)$ and $P_{4}=(1, -22.2)$ but not $P(12.5, -11.01)$ .

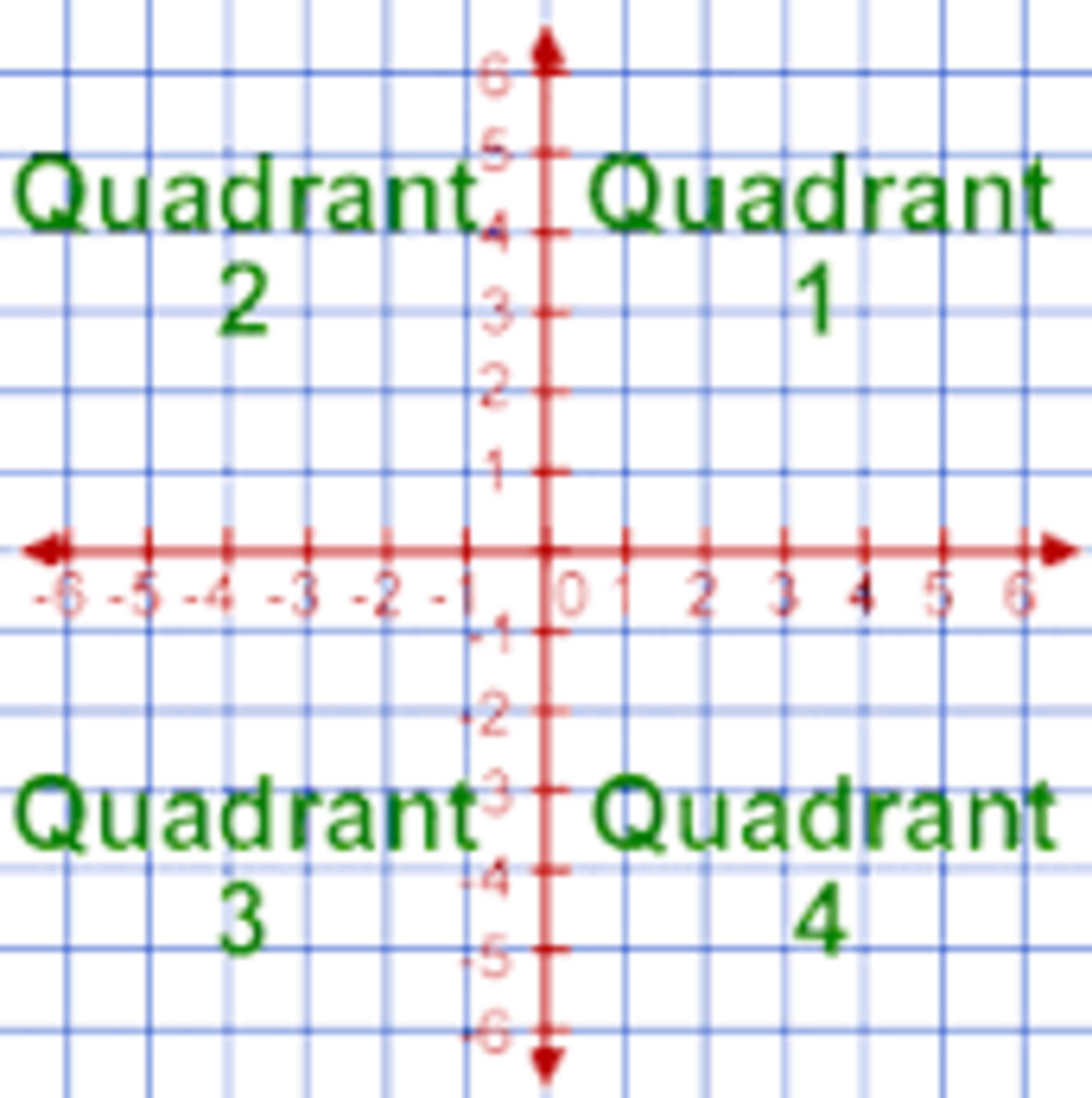
In this case, the quadrant 3 is said to be most dense because it contains more points (i-e: 2) than any other while the quadrant 1 is least dense because it contains least number of points (i-e: 0).

Let the Array be the array of real numbers and $m$ and $l$ be the most dense and least dense quadrant numbers respectively. $\text{ What is } m+l \, ?$

Details and Assumptions:

Points lying on either X-axis or Y-axis are not considered to be in any of the quadrants.
A point may repeat itself in the given array, consider such points as different and include them in your counting as well.

The answer is 5.

1 solution

Zeeshan Ali
Jan 15, 2016

Let G be the given array of size $n$ and S be an array of size 4 to store the number of points in each quadrant. Following algorithm does the desired work.

    S<-0 // initialize the array with 0

    // find the number of points lying in any quadrant
    for i<-0 to G.length
        if G[i]>0 and G[i+1]>0
            S[0]<-S[0]+1 // 1st quadrant
        else if G[i]<0 and G[i+1]>0
            S[1]<-S[2]+1 // 2nd quadrant
        else if G[i]<0 and G[i+1]<0
            S[2]<-S[2]+1 // 3rd quadrant
        else
            S[3]<-S[3]+1 // 4th quadrant
        i<-i+2

    // display the array 'S' to know the min and max values
    for i<-0 to 3
        print S[i]
        i<-i+1

The required value is min+max.

More fun with Arrays!

The answer is 5.

1 solution

0 pending reports