More fun with circles
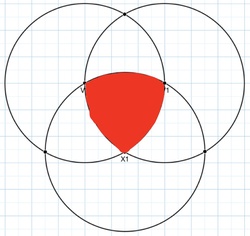 Three circles of radius 6 intersect eachother at their centers. The area of intersection, colored red, can be represented by
a
π
−
b
c
. Find a+b+c.
Three circles of radius 6 intersect eachother at their centers. The area of intersection, colored red, can be represented by
a
π
−
b
c
. Find a+b+c.
The answer is 39.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
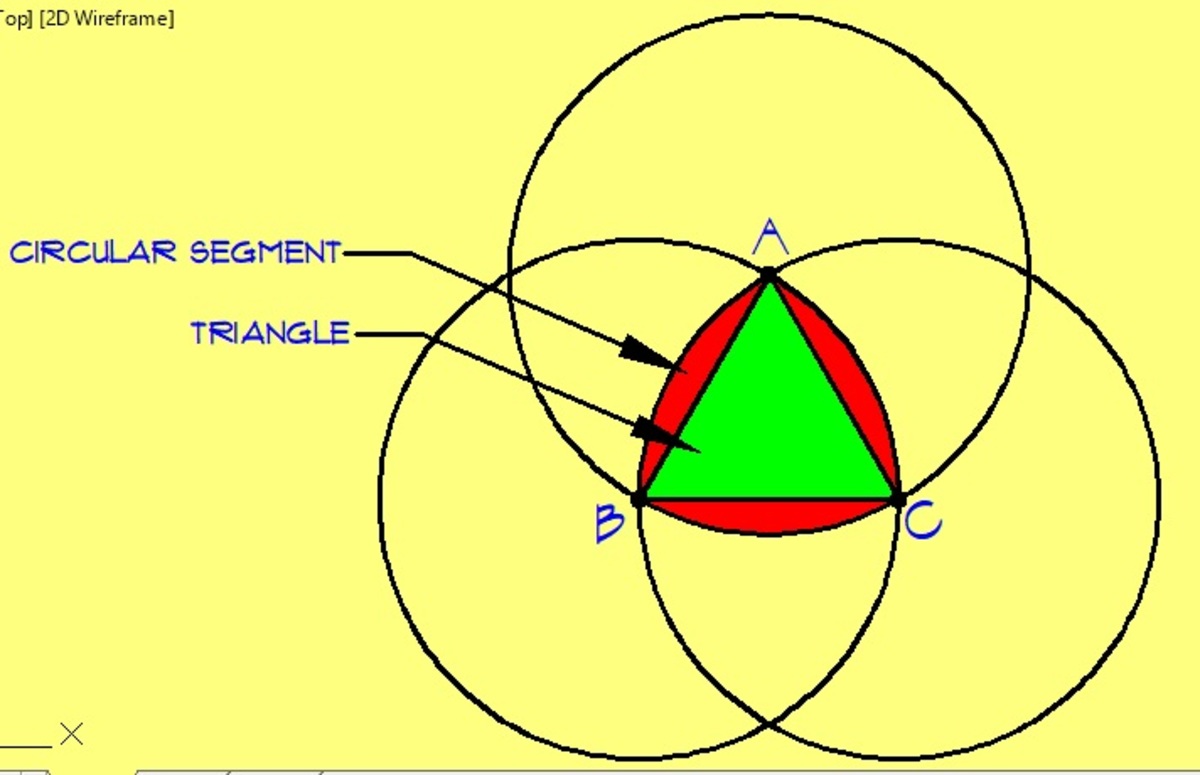
Let A , B and C be the centers of the three circles and S be the area of the shaded region.
Connect the centers of the three circles to form an equilateral triangle. Observed that the shaded region is composed of three circular segments and one equilateral triangle.
A s e g m e n t = A s e c t o r − A t r i a n g l e = 3 6 0 6 0 π ( 6 2 ) − 4 3 ( 6 2 ) = 6 π − 9 3
So the area of the shaded region is
S = 3 ( A s e g m e n t ) + A t r i a n g l e = 3 ( 6 π − 9 3 ) + 4 3 ( 6 2 ) = 1 8 π − 2 7 3 + 9 3 = 1 8 π − 1 8 3
The desired answer is 1 8 + 1 8 + 3 = 3 9
First, we start by drawing an equilateral triangle connecting the centers of each circle. Then we find the area of the 60 degree sector of minor arc VX 3 6 0 6 2 π ( 6 0 ) = 6 π .
Next we find the area of the sectors outside of the triangle but inside the intersection area. To do this, we subtract the area of the equilateral triangle from the sector that we just found and multiply it by three because there are three sections. 3 ( 6 π − 3 ∗ 3 3 ) ⇒ 1 8 π − 2 7 3 .
The last step is to add the area of the equilateral triangle 9 3 and our answer is 1 8 π − 1 8 3 . Thus a=18, b=18, and c=3 so 18+18+3= 3 9 .
The general formula for this problem (circles must intersect at centers or its much tougher)= 2 r 2 π − r 2 3 .
I think it would be great if all the problem solution writers on brilliant started to put a general formula at the bottom of their solution whenever possible (I know this isn't really possible for topics such as number theory, but it is quite often for geometry).