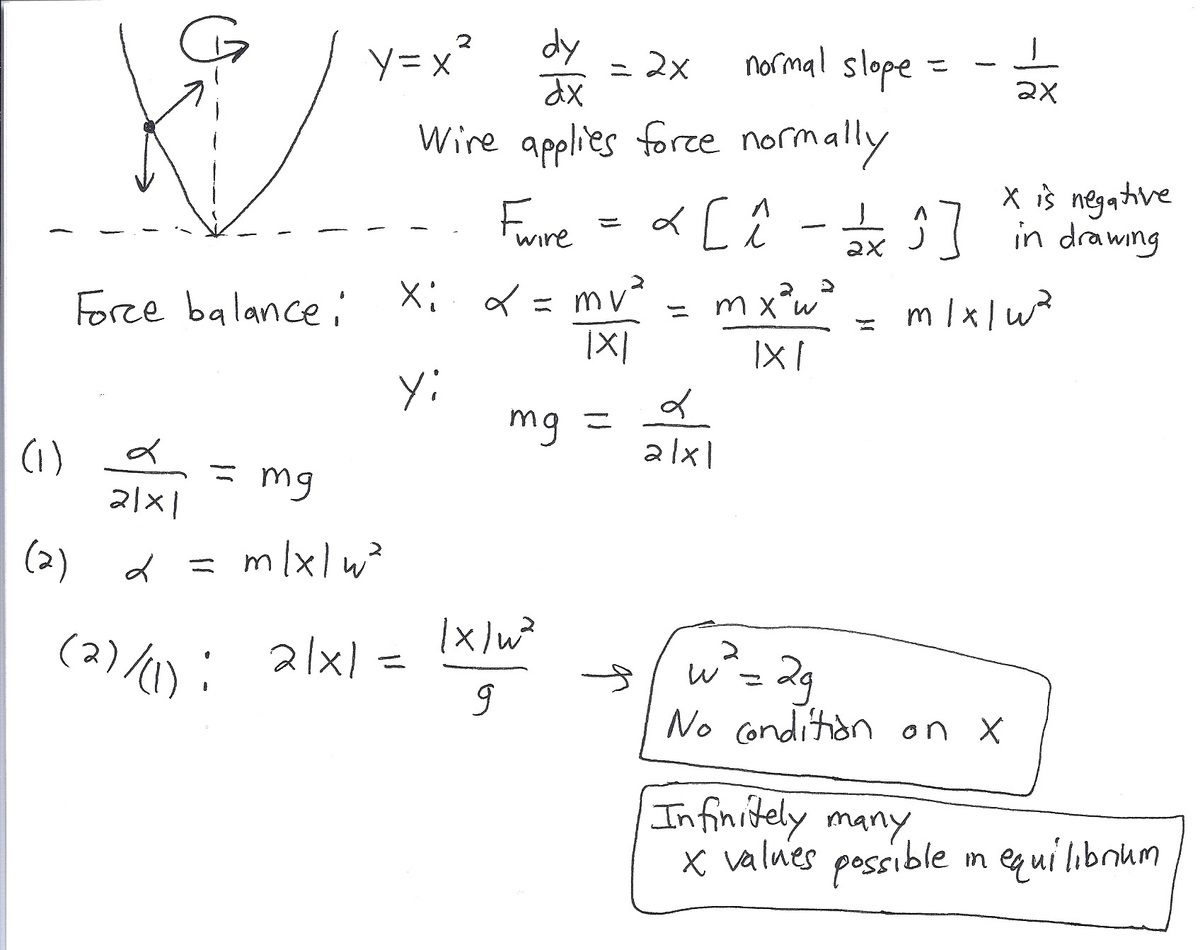
Floating beads in parabolic wires

Relevant wiki: Lagrangian Mechanics

An elegant way to approach this problem is through the Lagrangian formulation of mechanics. The natural coordinate system for this problem is a cylindrical system with $\mathbf{r} = \left(r,z,\theta\right)$ where $\theta$ is the angle around the $\hat{z}$ axis. The kinetic energy is given by the movement along the wire $\frac12m\left(\dot{r}^2 + \dot{h}^2\right)$ and the rotational kinetic energy $\frac12 m\dot{\theta}^2r^2$ . As the rotation of the wire is constant, we have $\dot{\theta} = \omega$ . Finally, the potential energy of the wire is given simply by $mgh$ .

We have $\begin{aligned} \mathcal{L} &= \mathcal{T} - \mathcal{U} \\ &= \frac12 m\left(\dot{h}^2 + \dot{r}^2 + r^2\omega^2\right) - mgh. \end{aligned}$ From the constraint $h = r^2$ , it can be shown that $\dot{h} = 2\dot{r}r.$ The lagrangian becomes $\mathcal{L} = \frac12 m\left(4r^2\dot{r}^2 + \dot{r}^2 + r^2\omega^2\right) - mgh.$ This is a lagrangian in one variable, so we have $\begin{aligned} \frac{d}{dt}\frac{\partial\mathcal{L}}{\partial\dot{r}} &= \frac{\partial\mathcal{L}}{\partial r} \\ m\ddot{r}\left(1 + 4r^2\right) &= 4m\dot{r}^2r + mr\left(\omega^2 - 2g\right). \end{aligned}$ When the bead is at steady state $\dot{r}$ and $\ddot{r}$ are zero and thus $\omega^2 = 2g.$ Note this places no condition on $r$ and so the bead can sit stably at any radius $r$ .

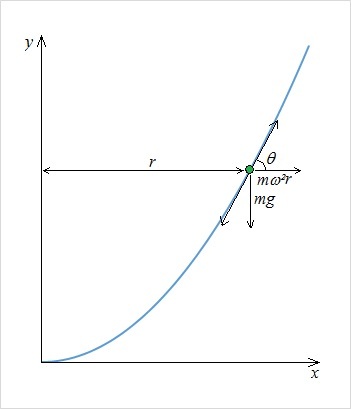
We note that the forces acting on the bead are its weight $mg$ and the centrifugal force $m \omega^2 r$ , where $r$ is the radius of rotation or the perpendicular distance of the bead from the axis ( $y$ -axis).

For the bead to maintain stationary relative to the frictionless wire, the following two forces up and down the wire are balanced:

$\begin{aligned} m \omega^2 r \cos \theta & = mg \sin \theta & \small \color{#3D99F6} \text{where } \tan \theta \text{ is the gradient of the wire at } x = r \\ m \omega^2 r & = mg \tan \theta \\ & = mg \times \frac {dy}{dx} \bigg|_{x=r} \\ & = mg \times 2x \bigg|_{x=r} \\ & = 2mgr \\ \implies \omega^2 & = 2g \end{aligned}$

We note that the condition for the bead to maintain a constant height is independent of $r$ , so it can be at any height on the wire. Therefore, the answer is $\boxed{\text{Infinitely many}}$ .

Here the parabola is the cross section of one of the equipotential surfaces (To visualize an equipotential surface, consider a tank full of water revolving about a vertical axis. The free surface of water - which is also an equipotential surface - assumes a paraboloidal shape). so it is like placing the bead on a flat ground and asking how many other points it can stay at? Infinite.