More Kissing Circles

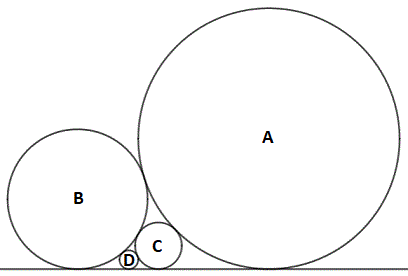
If the radius of B is $R$ and the radius of C is $r$ , then Descartes' Theorem tells us that the radii of A and D are $r_A \; = \; \frac{Rr}{(\sqrt{R} - \sqrt{r})^2} \hspace{2cm} r_D \; = \; \frac{Rr}{(\sqrt{R} + \sqrt{r})^2}$ respectively. The horizontal distance between the centres of A and D is therefore $2\sqrt{Rr_A} - 2\sqrt{Rr_D} \; = \; \frac{4Rr}{R-r}$ while the vertical distance between the centres of A and D is $r_A - r_D \; = \; \frac{4Rr\sqrt{Rr}}{(R-r)^2}$ If $L$ is the distance between the centres of A and D, we obtain the equation $L^2 \; = \; \frac{16R^2r^2}{(R-r)^2} + \frac{16R^3r^3}{(R-r)^4} \; = \; \frac{16R^2r^2(r^2-rR+ R^2)}{(R-r)^4}$ In this case $R=72$ and $L=1120$ , and we obtain the quartic equation $(r - 45)(143r^3 - 36936r^2 + 3048192r - 91445760) \; = \; 0$ The only real zero of the cubic term is $136.37...$ , and so (since we definitely have $r < 72$ ), we deduce that $r =\boxed{45}$ .

$(x_d-x_c)^2+(r_d-r_c)^2=(r_d+r_c)^2 \\$ $(x_a-x_c)^2+(r_a-r_c)^2=(r_a+r_c)^2 \\$ $(x_a-x_b)^2+(r_a-72)^2=(r_a+72)^2 \\$ $(x_d-x_a)^2+(r_d-r_a)^2=1120^2 \\$ $x_d^2+(72-r_d)^2=(72+r_d)^2\\$ $x_c^2+(72-r_c)^2=(72+r_c)^2 \\$ $x_b=0 \\$

And Wolframalpha use for this system wolframalpha , we see $r_c=45$ .