More magic!
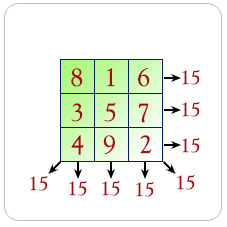
It is known that a magic square consists of a grid filled in with the digits 1-9 such that every column, row, and diagonal add up to the same constant (typically 15), as shown at right:
How many ways, though, can this be accomplished, including rotations and reflections?
The image shows one of the ways.
Image credit: https://www.w3resource.com
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The top left number can be chosen in 4 ways. (Any of the even numbers)
Once chosen, the bottom left number can be chosen in 2 ways.
After that, the rest of the numbers fall nicely into place.
This gives 4 ⋅ 2 = 8 ways.
Actually, this boils down to only one way, which can be reflected about either a diagonal and/or rotated to form the other 7.