Can You Name this Number?
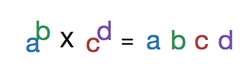 A student carelessly wrote a four digit number,
a
b
c
a
, on a piece of paper, instead of writing
a
b
×
c
a
. It so happened that the two figures had the same value. What was the 4 digit number
a
b
c
a
?
A student carelessly wrote a four digit number,
a
b
c
a
, on a piece of paper, instead of writing
a
b
×
c
a
. It so happened that the two figures had the same value. What was the 4 digit number
a
b
c
a
?
Details and Assumptions
a, b, and c are digits.
The answer is 2592.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
why did you us python (im not familiar with it)can u explain a little more briefly?
I feel the program below will greatly reduce the time.
for a in xrange(10):
b=9
c=9
if((a**b)*(c**a) < (1000*a+100*b+10*c+a)):
return
for b in range(9,1,-1):
c=9
if((a**b)*(c**a) == (1000*a+100*b+10*c+a)):
return
for c in range(9,1,-1):
if((a**b)*(c**a) == (1000*a+100*b+10*c+a)):
print a, b, c, a
Hi everyone. Firstly, the equation is a^b * c^a = abca. The method I used is an assumption. The range for all of the 4 digits is 1-9. So I made the assumption from the smallest digit.
Let a = 2.
So , the equation turns into
2^b * c^2 = 2bc2
From the equation, the answer is a four-digit-number.
Another assumption is made.
Let c = 9. The only reason to this is that putting the largest range of the number will decrease the time taken.
So, 2^b * 9^2 = 2bc2.
9^2 = 81.
The answer must be a four digits containing 2 in the front and another 2 at the back.
Let b = 9.
2^9 = 2080. The multiplication of 2080 and 81 has exceeded the range for the answer which is a four-digits-number containing 2 in the front and 2 at the back.
The following assumptions are made by decreasing the power of 2. Until the the following assumption, 2^5.
2^5 = 32.
32*81 = 2592.
The answer 2592 is correct as the arrangement of the combination of numbers, which is
a^b*c^a=abca
2^5*9^2=2592
a=2
b=5
c=9
This is the method I used to solve this problem. If anyone finds this wrong, please give me some feedback for me to improve myself.
The method I used is assumptions. I hope all of you who can solve the problem with other methods, do write your solutions here for me and the others to learn for more.
My name is TAN JIA JIN, and I come from Malaysia. Thank you. Have a nice day.
Sincerely, TAN.
You have a good solution and correct. I have solved it a little different. You will find the solution below. Best wishes.
1 2 3 4 5 6 7 |
|
You didn't really need the variable d, but otherwise great solution! I did it exactly the same except with 3 for loops.
Python:
1 2 3 4 5 6 7 |
|
Great code !!!
I'm too lazy to write codes, and i like "drag and drop" so... :P
0.04 second , fast enough for me. :P
Java solution -
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
Execution time ~0.002 second
I have used a java code to find the number.
1 2 3 4 5 |
|
The easiest approach would be to assume values of a and try for
b
=
c
=
9
a
n
d
s
e
e
i
f
a
9
∗
9
a
is a four digit number. If not got to next value of a. For a =0, 1, we do not get a four digit number.
Next
a
=
2
.
2
9
∗
9
2
=
4
1
4
7
2
We get a number greater than four digits.
b
=
8
,
2
8
∗
9
2
=
2
0
7
3
6
.
.
N
O
…
b
=
7
,
2
7
∗
9
2
=
1
0
3
6
8
.
.
N
O
.
.
b
=
6
,
6
8
∗
9
2
=
5
1
8
4
.
.
i
t
i
s
f
o
u
r
d
i
g
i
t
s
,
b
u
t
n
o
t
a
s
w
e
d
e
s
i
r
e
.
b
=
5
,
2
5
∗
9
2
=
2
5
9
2
…
.
.
2
5
9
2
I used Python code
Output