More of a project than a problem - Part 2

Using the following code, the result for $a = 2$ , $b = 3$ , and $c = 5$ is $S \approx \boxed{122.727}$ .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

# Brilliant - More of a Project than a Problem - Part 2
# Python 2.7.3

import math

# number of cylindrical slices
m = 1000000

# dimensions of cuboid, and space diagonal vector is (a, b, c)
a = 2
b = 3
c = 5

# equation perpendicular to (a, b, c) at (at, bt, ct) is 
#   ax + by + cz = dt with the following d value.
d = a ** 2 + b ** 2 + c ** 2

# find the surface area of each cylindrical slice and keep a running total 
totals = 0
maxr = 0
for t1 in range(0, 1 * m):
    t = 1.0 * t1 / m

    # save the value of the last maxr for the surface area equation
    maxr_old = maxr

    # find the maximum radius for the cylindrical slice by testing all
    #   12 line segments of the cuboid that intersect ax + by + cz = dt,
    #   the equation of the plane perpendicular to (a, b, c) at (at, bt, ct)
    maxr = 0

    # test intersection of planes x = 0 and y = 0, x = 0 and y = b,
    #   x = a and y = 0, and x = a and y = b for possible maxr
    for x in range(0, a + 1, a):
        for y in range(0, b + 1, b):
            z = 1.0 * (d * t - a * x - b * y) / c
            r = math.sqrt((a * t - x) ** 2 + (b * t - y) ** 2 + (c * t - z) ** 2)
            if z >= 0 and z <= c and r > maxr:
                maxr = r

    # test intersection of planes x = 0 and z = 0, x = 0 and z = c,
    #   x = a and z = 0, and x = a and z = c for possible maxr
    for x in range(0, a + 1, a):
        for z in range(0, c + 1, c):
            y = 1.0 * (d * t - a * x - c * z) / b
            r = math.sqrt((a * t - x) ** 2 + (b * t - y) ** 2 + (c * t - z) ** 2)
            if y >= 0 and y <= b and r > maxr:
                maxr = r

    # test intersection of planes y = 0 and z = 0, y = 0 and z = c,
    #   y = b and z = 0, and y = b and z = c for possible maxr
    for y in range(0, b + 1, b):
        for z in range(0, c + 1, c):
            x = 1.0 * (d * t - b * y - c * z) / a
            r = math.sqrt((a * t - x) ** 2 + (b * t - y) ** 2 + (c * t - z) ** 2)
            if x >= 0 and x <= a and r > maxr:
                maxr = r

    # find the surface area of the cylindrical slice with the lateral area
    #   equation pi * (r1 + r2) * sqrt((r1 - r2)**2 + h**2) using r1 = maxr,
    #   r2 = maxr_old, and h = sqrt(d) / m; and then add it to the total
    s = 1.0 * math.pi * (maxr + maxr_old) * math.sqrt((
        maxr - maxr_old) ** 2 + 1.0 * d / m ** 2)
    totals += s

# display the surface area total
print "The surface area of revolution is %0.3f" % totals + "."

This one makes use of much of the machinery of the previous problem. The differences are at the end. Here is my process:

Let the space diagonal be between points $(0,0,0)$ and $(2,3,5)$ . Let $\vec{u}$ be a unit vector along the space diagonal, and let $\vec{u_1}$ and $\vec{u_2}$ be unit vectors perpendicular to $\vec{u}$ .

Let the parameter $\alpha$ be the distance along the space diagonal. Let the value $\sigma$ be the perpendicular distance from a point on the space diagonal to some place on the cuboid. Let $\theta$ be an angular parameter.

$\vec{u_3} = cos \theta \, \vec{u_1} + sin \theta \, \vec{u_2} \\ \text{Point on Cuboid Surface} = \alpha \, \vec{u} + \sigma \, \vec{u_3}$

Now, the tricky part is that for each $\alpha$ , $\theta$ varies continuously between $0$ and $2 \pi$ . Consequently, there are infinitely many $\sigma$ values for each $\alpha$ . The processing is as follows:

1) For every $\alpha$ between $0$ and the length of the space diagonal (in small steps), sweep $\theta$ from $0$ to $2 \pi$ in small steps.
2) For every $\theta$ , form $\vec{u_3}$ and determine a $\sigma$ value corresponding to the intersection with the infinite plane containing each cuboid face. There will be six $\sigma$ calculations in total.
3) The intersection point with the cuboid corresponds to the smallest positive $\sigma$ value. Call this $\sigma_{intersect}$
4) For each $\alpha$ , as $\theta$ is swept, keep track of the largest value of $\sigma_{intersect}$ . Call this $\sigma_{max}$

This is where the old solution ends and the new solution begins

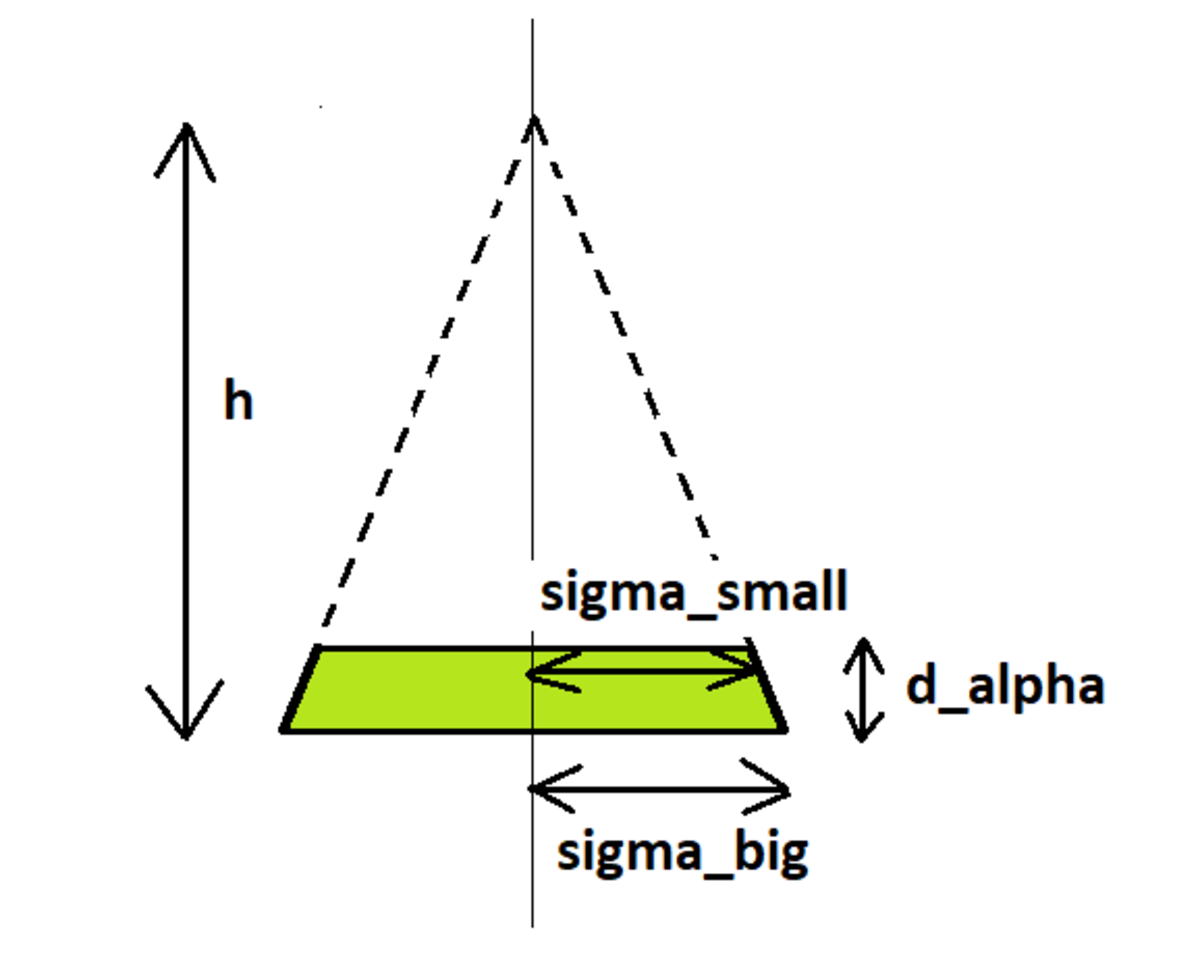
5 ) Every time we increment $\alpha$ , we need to calculate a new value of $\sigma_{max}$ and construct a partial cone according to the diagram below. We have to use the new value of $\sigma_{max}$ and the old (stored) value of $\sigma_{max}$ to do this.

6) Call the larger value of the two $\sigma_{big}$ and the smaller value $\sigma_{small}$ .
7) Find the height of the cone from the proportionality $\large{\frac{d \alpha}{\sigma_{big} - \sigma_{small}} = \frac{h}{\sigma_{big}}}$
8) The surface area of the "cone slice" is equal to the lateral surface area of the total cone of height $h$ , minus the lateral surface area of the smaller cone of height $h - d\alpha$ .
9) The slant heights of the two cones are $\sqrt{h^2 + \sigma_{big}^2}$ and $\sqrt{(h-d\alpha)^2 + \sigma_{small}^2}$
10) The surface areas of the two cones are $\pi \, \sigma_{big} \,\sqrt{h^2 + \sigma_{big}^2}$ and $\pi \, \sigma_{small} \,\sqrt{(h-d\alpha)^2 + \sigma_{small}^2}$
11) The infinitesimal surface area is $\pi \, \sigma_{big} \,\sqrt{h^2 + \sigma_{big}^2} - \pi \, \sigma_{small} \,\sqrt{(h-d\alpha)^2 + \sigma_{small}^2}$
12) Adding up all of the infinitesimal surface areas of the partial cones yields a total surface area of revolution of about $122.7$

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172

import math

##################################

Num = 4*10**3

##################################

vx = 2.0
vy = 3.0
vz = 5.0

v = math.sqrt(vx**2.0 + vy**2.0 + vz**2.0)

v1x = 1.0
v1y = 1.0
v1z = -1.0

v1 = math.sqrt(v1x**2.0 + v1y**2.0 + v1z**2.0)

v2x = -8.0
v2y = 7.0
v2z = -1.0

v2 = math.sqrt(v2x**2.0 + v2y**2.0 + v2z**2.0)

##################################

ux = vx / v
uy = vy / v
uz = vz / v

u1x = v1x / v1
u1y = v1y / v1
u1z = v1z / v1

u2x = v2x / v2
u2y = v2y / v2
u2z = v2z / v2

##################################

print (ux**2.0 + uy**2.0 + uz**2.0)
print (u1x**2.0 + u1y**2.0 + u1z**2.0)
print (u2x**2.0 + u2y**2.0 + u2z**2.0)

print ""

print (ux*u1x + uy*u1y + uz*u1z)
print (ux*u2x + uy*u2y + uz*u2z)
print (u1x*u2x + u1y*u2y + u1z*u2z)

print ""


##################################

dalpha = v / Num
dtheta = 2.0 * math.pi / Num

##################################

xref_left = 0.0
xref_right = 2.0

yref_up = 3.0
yref_down = 0.0

zref_bottom = 0.0
zref_top = 5.0

####################################################################

S = 0.0

alpha = 0.0

count = 0

while alpha <= v:

    ####

    if count == 0:
        sigma_max_store = 0.0
    else:
        sigma_max_store = sigma_max

    ####

    alpha = alpha + dalpha

    x0 = alpha * ux
    y0 = alpha * uy
    z0 = alpha * uz

    theta = 0.0

    sigma_max = -999999.0

    while theta <= 2.0 * math.pi:

        u3x = math.cos(theta) * u1x + math.sin(theta) * u2x
        u3y = math.cos(theta) * u1y + math.sin(theta) * u2y
        u3z = math.cos(theta) * u1z + math.sin(theta) * u2z

        #####

        sigma_x_left = (xref_left - x0)/u3x
        sigma_x_right = (xref_right - x0)/u3x

        sigma_y_up = (yref_up - y0)/u3y
        sigma_y_down = (yref_down - y0)/u3y

        sigma_z_bottom = (zref_bottom - z0)/u3z
        sigma_z_top = (zref_top - z0)/u3z

        #####

        if sigma_x_left < 0.0:
            sigma_x_left = 10.0**12.0

        if sigma_x_right < 0.0:
            sigma_x_right = 10.0**12.0

        if sigma_y_up < 0.0:
            sigma_y_up = 10.0**12.0

        if sigma_y_down < 0.0:
            sigma_y_down = 10.0**12.0

        if sigma_z_bottom < 0.0:
            sigma_z_bottom = 10.0**12.0

        if sigma_z_top < 0.0:
            sigma_z_top = 10.0**12.0

        #####

        sigma_intersect = min(sigma_x_left,sigma_x_right,sigma_y_up,sigma_y_down,sigma_z_bottom,sigma_z_top)

        #####

        if sigma_intersect > sigma_max:
            sigma_max = sigma_intersect

        #####

        theta = theta + dtheta

    sigma_big = max(sigma_max,sigma_max_store)
    sigma_small = min(sigma_max,sigma_max_store)

    delta_sigma = sigma_big - sigma_small

    h = sigma_big * dalpha / delta_sigma

    L_big = math.hypot(sigma_big,h)
    L_small = math.hypot(sigma_small,h-dalpha)

    LSA_big = math.pi * sigma_big * L_big
    LSA_small = math.pi * sigma_small * L_small

    dS = LSA_big - LSA_small

    S = S + dS

    count = count + 1

####################################################################

print S