More of Circles and Squares.
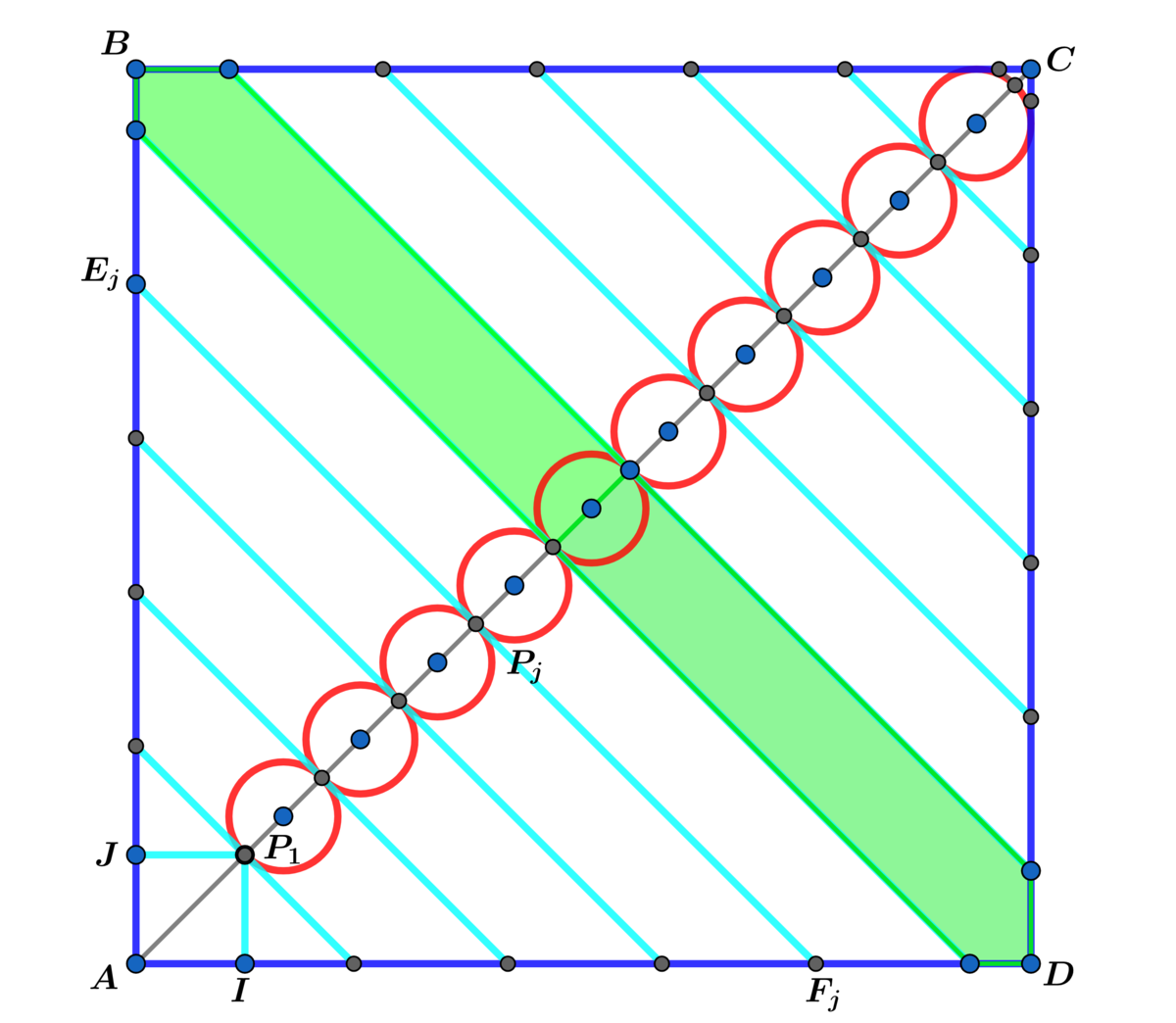
Extend the above diagram to congruent circles where is a even positive integer.
In square , one of the vertices of square touches at and is tangent to circle at for each integer , where and the radius of each congruent circle is half the side of the square .
Let be the area of the shaded green region.
Find the value of for which
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let n be a fixed even integer, a a side of square A B C D and x a side of square A J P 1 I .
Extending the diagram to even n congruent circles we obtain:
2 a = 2 x + ( n − 1 ) x + 2 x + 2 x ⟹ 4 a = ( 6 + 2 ( 2 n − 1 ) ) x ⟹
x = 6 + 2 ( 2 n − 1 ) 4 a = 2 ( 3 2 + ( 2 n − 1 ) ) 4 a = 3 2 + ( 2 n − 1 ) 2 2 a
C P 2 n + 1 = ( n − ( 2 n + 1 ) + 2 1 + 2 1 ) x = ( 2 2 2 n + 2 − 2 ) ( 2 n + 3 2 − 1 2 2 ) a =
2 n + 3 2 − 1 2 ( n + 2 − 1 ) a ⟹ A △ 1 = ( C P 2 n + 1 ) 2 = ( 2 n + 3 2 − 1 ) 2 2 ( n + 2 − 1 ) 2 a 2
A P 2 n = ( 2 + ( 2 n − 1 ) ) x = ( 2 n + 2 ( 2 − 1 ) ) ( 2 n + 3 2 − 1 2 2 ) a =
2 n + 3 2 − 1 2 ( n + 2 ( 2 − 1 ) ) a ⟹ A △ 2 = ( A P 2 n ) 2 = ( 2 n + 3 2 − 1 ) 2 2 ( n + 2 ( 2 − 1 ) ) 2 a 2
⟹ A △ 1 + A △ 2 = ( 2 n + 3 2 − 1 ) 2 2 ( 2 n 2 + 6 ( 2 − 1 ) n + 5 ( 3 − 2 2 ) ) a 2 ⟹ A T = a 2 − ( A △ 1 + A △ 2 ) ⟹
A △ A B C D A T = ( 2 n + 3 2 − 1 ) 2 8 n + 1 4 2 − 1 1 = 9 3 2 2 − 4 1
⟹ ( 1 2 8 2 − 1 6 4 ) n 2 + ( 8 6 0 − 6 2 0 2 ) n + 7 2 8 2 − 1 0 6 4 = 0 ⟹
n = 2 ( 1 2 8 2 − 1 6 4 ) − ( 8 6 0 − 6 2 0 2 ) ± ( 2 0 4 − 1 0 8 2 )
For ( + ) : n = 2 ( 1 2 8 2 − 1 6 4 ) − 6 5 6 + 5 1 2 2 = 2 ( 1 2 8 2 − 1 6 4 ) 4 ( 1 2 8 2 − 1 6 4 ) = 2
For ( − ) : n = 3 6 7 3 7 1 − 5 2 5 2 < 0 ∴ dropping negative irrational root ⟹ n = 2 .