More on Comparing Areas
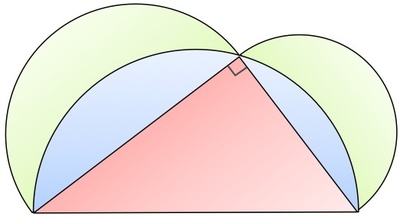 Semicircles were constructed on the sides of a right triangle as shown in the figure . Let
and
represents the green area and the red area respectively. Compare the red and the green areas?
Semicircles were constructed on the sides of a right triangle as shown in the figure . Let
and
represents the green area and the red area respectively. Compare the red and the green areas?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the side lengths of the right triangle be a , b , and c , where c is the hypotenuse and the blue area be B . Then the blue area is given by:
B ⟹ R = 4 π c 2 − R = 4 π c 2 − B
and the green area:
G = 4 π a 2 + 4 π a 2 − B = 4 π c 2 − B Since a 2 + b 2 = c 2
Therefore, G = R .