More Paraboloid Surface Dynamics
 A particle of mass
is sliding on a smooth surface in the shape of a paraboloid with equation
(for some arbitrary distance
), with the positive
-axis pointing vertically upwards. There is a constant gravitational force of magnitude
on the particle, acting vertically downwards.
A particle of mass
is sliding on a smooth surface in the shape of a paraboloid with equation
(for some arbitrary distance
), with the positive
-axis pointing vertically upwards. There is a constant gravitational force of magnitude
on the particle, acting vertically downwards.
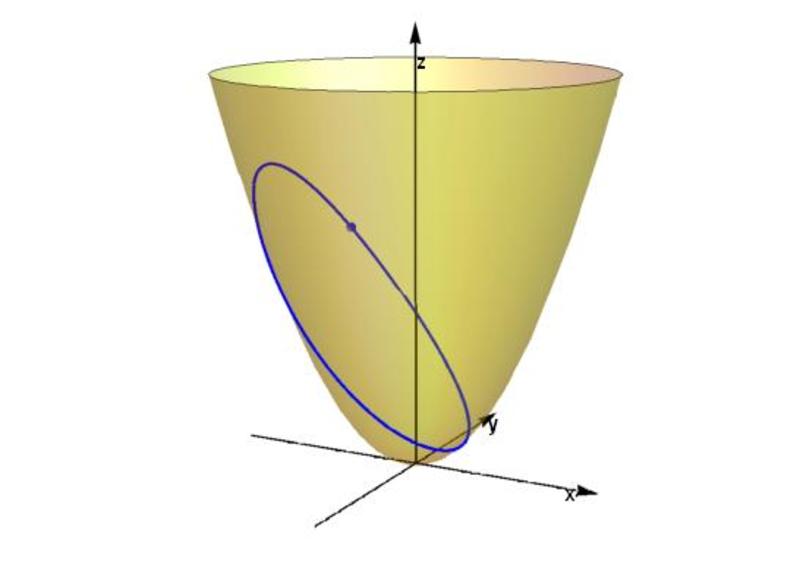
Initially the particle is at a point on the paraboloid with height , and is moving horizontally on the surface with instantaneous speed , where . Define the quantity There is a unique value of for which the orbit of the particle is a simple periodic loop, so that the particle rises from its initial height of to its maximum height, and returns to its initial height while performing precisely one orbit around the paraboloid, as shown in the diagram. If this particular value of is , find the value of .
The answer is 1193897.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Working in cylindrical polar coordinates, the position vector of the particle can be written as r = ⎝ ⎛ 2 a z cos θ 2 a z sin θ z ⎠ ⎞ Differentiating with respect to t we obtain the kinetic energy of the particle T = 2 1 m ( 1 + z a ) z ˙ 2 + 2 m a z θ ˙ 2 Since the potential energy of the particle is V = m g z we obtain the Lagrangian L = 2 1 m ( 1 + z a ) z ˙ 2 + 2 m a z θ ˙ 2 − m g z Initially we know that r = 2 a , z = a , r ˙ = z ˙ = 0 and θ ˙ = ω . Since L is independent of θ , we deduce that ∂ θ ˙ ∂ L is constant, and we deduce that z θ ˙ = a ω . The second equation of motion is 0 = d t d ( ∂ z ˙ ∂ L ) − ∂ z ∂ L = d t d [ m ( 1 + z a ) z ˙ ] + 2 z 2 m a z ˙ 2 − 2 m a θ ˙ 2 + m g = m ( 1 + z a ) z ¨ − 2 z 2 m a z ˙ 2 − z 2 2 m a 3 ω 2 + m g = d z d [ 2 1 m ( 1 + z a ) z ˙ 2 + z m g α a 2 + m g z ] so that 2 1 m ( 1 + z a ) z ˙ 2 + z m g α a 2 + m g z = m g a ( α + 1 ) and hence z ˙ 2 = a + z 2 g ( α a − z ) ( z − a ) Thus the particle oscillates between height z = a and z = α a with period T = 2 ∫ a α a 2 g ( α a − z ) ( z − a ) a + z d z Using the substitution z = a ( cos 2 θ + α sin 2 θ ) , we obtain T = 2 ∫ 0 2 1 π 2 g a + a ( cos 2 θ + α sin 2 θ ) 2 d θ = 2 g 2 a ∫ 0 2 1 π 1 + cos 2 θ + α sin 2 θ d θ = 2 g 2 a ∫ 0 2 1 π 2 + ( a − 1 ) sin 2 θ d θ = 4 g a E ( − 2 α − 1 ) where E is the complete elliptic integral.
During a half period the particle moves through an angle Θ ( α ) , where Θ ( α ) = ∫ a α a d z d θ d z = ∫ a α a z ˙ θ ˙ d z = a ω ∫ a α a z z ˙ d z = a ω ∫ a α a 2 g ( α a − z ) ( z − a ) a + z z d z = ω g 2 a ∫ 0 2 1 π cos 2 θ + α sin 2 θ 1 + cos 2 θ + α sin 2 θ d θ = α ∫ 0 2 1 π 1 + ( α − 1 ) sin 2 θ 2 + ( α − 1 ) sin 2 θ d θ = 2 α [ K ( − 2 α − 1 ) + Π ( − ( α − 1 ) , − 2 α − 1 ) ] where K is the complete elliptic integral of the first kind, while Π is the complete elliptic integral of the third kind.