More Pizza!
Ahmed and Omar are really hungry for some pizza. They agree to share a triangular piece of pizza of area 360, based on the following division scheme:
-
Ahmed chooses a point D inside the pizza.
-
Omar then makes a straight cut through D and chooses one part of the pizza after cutting.
If both of them want to maximize the amount of pizza that they get, what is the maximum area of pizza that Omar can get?
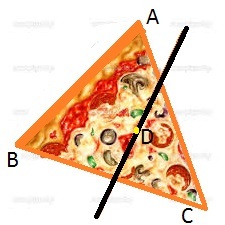
The answer is 200.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Claim: For any point D, Omar has a straight cut which gives him at least 5/9 of the pizza.
Proof: Take a triangle plot with vertices A, B, C, and grid lines parallel to AB, BC, CA.
For any point D within the triangle, draw in these grid lines, which cut AB, BC and CA.
Let A B be the point where the line parallel to the side opposite B cuts the side opposite A , with the other points similarly defined.
Define x = ∣ B C ∣ ∣ A B A C ∣ to be the fractional part that is cut out along line B C , y = ∣ C A ∣ ∣ B A B C ∣ and z = ∣ A B ∣ ∣ C B C A ∣ respectively.
Observe that x + y + z = ∣ B C ∣ ∣ A B A C ∣ + ∣ C A ∣ ∣ B A B C ∣ + ∣ A B ∣ ∣ C B C A ∣ = ∣ B C ∣ ∣ A B A C ∣ + ∣ B C ∣ ∣ C A B ∣ + ∣ B C ∣ ∣ A C B ∣ = 1 .
Without loss of generality, x ≥ 3 1 . Then, Omar makes the cut C A B A ), and picks the slice B C B A C A . The fractional area of A B A C A is ( 1 − x ) 2 , so the fractional area of Omar's slice is given by 1 − ( 1 − x ) 2 = 2 x − x 2 ≥ 9 5
Hence, Omar has a cut that yields at least 5/9 of the pizza.
Note: We see that if Omar is restricted to these cuts, then he can only guarantee 5/9 of the pizza if x = y = z = 3 1 , which happens when D is the centroid of the pizza. This leads to the next claim
Claim: If Ahmed picks the centroid of the pizza, the best that Omar can do is 5/9 of the pizza.
Proof: Say Omar picks a cut, which intersects the perimeter of the triangle at E and F . If D E = E F , then by tilting the cut further, Omar can increase the size of the slice that he picks.
As an explicit example, suppose Omar makes the cut EF and picks the slice B C E F . Then, since D E < D F , we can tilt the line about D, to E ′ F ′ . Comparing areas, since △ D E E ′ < △ D F F ′ , hence B C E ′ F ′ > B C E F . Note: If Omar picks the slice A E F , then he should tilt in the opposite direction.
This tilting no longer results in a larger area when D E = D F . Hence, when Omar maximizes his slice, we must have D E = E F .
Since D is the centroid, this implies that E F is parallel to one of the sides of the triangle. Then, from the above analysis, since we have x = y = z = 3 1 , thus the largest slice that Omar can pick has fractional area 1 − ( 1 − 3 1 ) 2 = 9 5 .