More Symmetrical
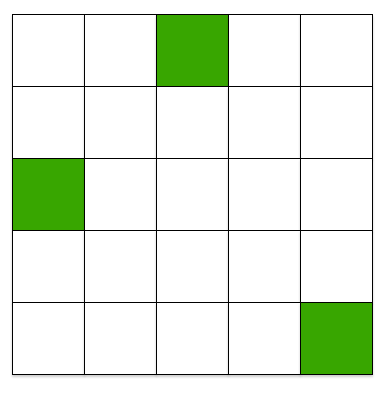
What is the minimum number of additional unit squares that have to be shaded green in the above figure, in order for there to be (at least) two lines of symmetry?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We will approach this problem exhaustively.
For a square, there are only 4 possible symmetries, which are vertical, horizontal, top left to bottom right, and top right to bottom left. On the 5 × 5 grid, the possible lines of symmetry look like this:
Now, if a grid has both verticle/horizontal and diagonal symmetry, then the grid has all 4 symmetries. To prove this, let's put the grid on a coordinate axis with its center at ( 0 , 0 ) , like so:
Now, let us construct a grid that has vertical and top left to bottom right symmetry. On our coordinate plane, this means that the grid is symmetrical over the line x = 0 (vertical symmetry) and the line y = − x (diagonal symmetry). If we have a point on our grid ( x , y ) which is shaded in, then by vertical symmetry (a reflection over the line x = 0 ) the point ( − x , y ) must also be shaded in on our grid. Applying diagonal symmetry (a reflection over the line y = − x ) results in two new points: ( x , y ) gives ( − x , − y ) and ( − x , y ) gives ( x , − y ) . We now have 4 points. The result looks like this:
In this picture, the original point is U, and the 3 other points are the result of reflections. This grid obeys all four symmetries, therefore if a grid obeys a vertical/horizontal symmetry and a diagonal symmetry, it obeys all four symmetries. This means that there are only 7 possible combinations of lines of symmetry: vertical, horizontal, top left to bottom right, top right to bottom left, top left to bottom right AND top right to bottom left, vertical AND horizontal, and all 4 lines of symmetry.
Since we want the grid to obey at least 2 symmetries, the symmetries must be one of the following: top left to bottom right AND top right to bottom left, vertical AND horizontal, and all symmetries. We test the three possible cases:
Case 1: Symmetry along both diagonals:
3 squares added.
Case 2: For vertical AND horizontal symmetry:
5 squares added. Note that because the grid already had diagonal symmetry, adding vertical symmetry results in a grid which has all four symmetries, meaning we don't have to test the case of all 4 symmetries.
The answer is therefore 3, by exaustion.