More Tangents
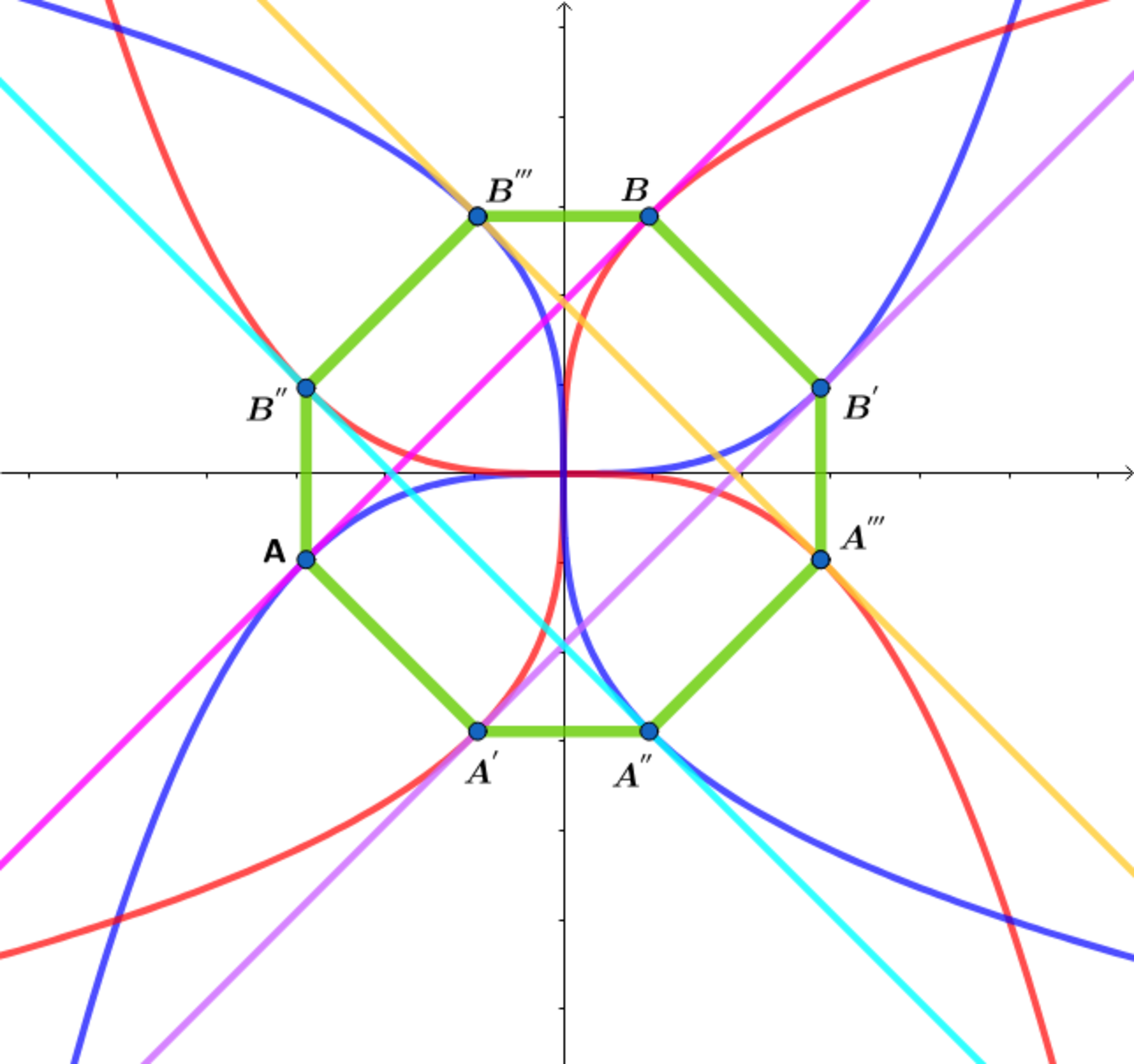
If A B and A ′ B ′ are tangent to the curves y = x 1 / 3 and y = x 3 at points A , B , A ′ , B ′ and A ′ ′ B ′ ′ and A ′ ′ ′ B ′ ′ ′ are tangent to the curves y = − x 1 / 3 and y = − x 3 at points A ′ ′ , B ′ ′ , A ′ ′ ′ ′ , B ′ ′ ′ and the area of the octagon formed by connecting the eight points above can be expressed as A o c t a g o n = c c a a ∗ b , where a , b and c are distinct primes, find a + b + c .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Let f ( x ) = x 3 and g ( x ) = x 3 1 ⟹ d x d ( f ( x ) ) ∣ x = a = 3 a 2 and d x d ( g ( x ) ) ∣ x = b = 3 b 3 2 1 ⟹ 3 a 2 = 3 b 3 2 1 ⟹ a = ± 3 b 3 1 1
Using point A : ( 3 b 3 1 − 1 , 2 7 b − 1 ) and B : ( b , b 3 1 ) ⟹ slope m A B = 9 b 3 2 ( 3 b 3 4 + 1 ) 2 7 b 3 4 + 1 = 3 b 3 2 1 ⟹ b = 3 2 3 1 ⟹ a = 3 2 1 − 1 ⟹
A : ( 3 2 1 − 1 , 3 2 3 − 1 ) and B : ( 3 2 3 1 , 3 2 1 1 ) ⟹ m A B = 1 ⟹ y = x + 3 2 3 2
Using the symmetry about the line y = x ⟹
A ′ : ( 3 2 3 − 1 , 3 2 1 − 1 ) and B ′ : ( 3 2 1 1 , 3 2 3 1 ) ⟹ m A ′ B ′ = 1 ⟹ y = x − 3 2 3 2
Using the symmetry about the y axis ⟹
A ′ → A ′ ′ = ( 3 2 3 1 , 3 2 1 − 1 ) and B ′ → B ′ ′ = ( 3 2 1 − 1 , 3 2 3 1 )
Using the symmetry about the line y = − x ⟹
A ′ ′ → A ′ ′ ′ = ( 3 2 1 1 , 3 2 3 − 1 ) and B ′ ′ → B ′ ′ ′ = ( 3 2 3 − 1 , 3 2 1 1 ) .
A B ′ ′ = 3 3 2 = A ′ A ′ ′ = B B ′ ′ ′ = A ′ ′ ′ B ′
and,
A A ′ = 3 2 3 2 = B B ′ = B ′ ′ B ′ ′ ′ = A ′ ′ A ′ ′ ′
For △ B ′ ′ ′ O B ⟹ A △ B ′ ′ ′ O B = 2 1 ( B B ′ ′ ′ ) ( O M ∗ ) = 2 1 ( 3 3 2 ) ( 3 1 ) = 9 1
For △ A O A ′ the midpoint M of A A ′ is M : ( 3 3 − 2 , 3 3 − 2 ) ⟹ O M = 3 2 3 2 ⟹
A △ A O A ′ = 2 1 ( A A ′ ) ( O M ) = 2 1 ( 3 2 3 2 ) 2 = 2 7 4
∴ A o c t a g o n = 4 ( 9 1 + 2 7 4 ) = 4 ( 2 7 7 ) = 3 3 2 2 ∗ 7 = c c a a ∗ b ⟹ a + b + c = 1 2 .
Consider the graphs of y = x 3 and y = x 1 / 3 . As these functions are inverses, they are reflections of each other across the line y = x . However, they are both also odd functions. The combination of these two facts means that they are also reflections of each other across the line y = − x , and therefore lines A B and A ′ B ′ are both perpendicular to y = − x , i.e they both have slope 1. Likewise, lines A ′ ′ B ′ ′ and A ′ ′ ′ B ′ ′ ′ have slope -1.
Deriving y = x 3 and setting this derivative equal to 1 will lead us to the coordinates of points A and B ′ .
y ′ = 3 x 2 = 1 ⇒ x = ± 3 1 ⇒ y = ± 3 3 1
Thus A has coordinates ( 3 − 1 , 3 3 − 1 ) and B ′ has coordinates ( 3 1 , 3 3 1 ) .
Using the same technique with the other three functions, we find the coordinates of all eight points of the octagon.
A ( 3 − 1 , 3 3 − 1 ) ; A ′ ( 3 3 − 1 , 3 − 1 ) ; A ′ ′ ( 3 3 1 , 3 − 1 ) ; A ′ ′ ′ ( 3 1 , 3 3 − 1 )
B ( 3 3 1 , 3 1 ) ; B ′ ( 3 1 , 3 3 1 ) ; B ′ ′ ( 3 − 1 , 3 3 1 ) ; B ′ ′ ′ ( 3 3 − 1 , 3 1 )
The equation of line A A ′ is clearly x + y = 3 3 − 4 ; its x -intercept is 3 3 − 4 . The equation of line B ′ ′ B ′ ′ ′ is clearly x − y = 3 3 − 4 ; its x -intercept is also 3 3 − 4 . Thus lines A A ′ and B ′ ′ B ′ ′ ′ intersect on the negative half of the x -axis, let's say at P .
In the same way we can see that lines A A ′ and A ′ ′ A ′ ′ ′ intersect on the negative half of the y -axis, say at Q ; lines A ′ ′ A ′ ′ ′ and B B ′ intersect on the positive half of the x -axis, let's say at R ; and finally lines B B ′ and B ′ ′ B ′ ′ ′ intersect on the positive half of the y -axis, let's say at S .
Then P Q R S must be a square. P R is a diagonal of the square, and its length d is clearly 3 3 8 . Then we can find the area of P Q R S to be 2 d 2 = 2 7 3 2 .
To find the area of the octagon in question, we must remove the four corners of square P Q R S . Consider one of those four corners, the triangle A B ′ ′ P . It is a right isosceles triangle with hypotenuse of length h = 3 3 2 . Then the area of triangle A B ′ ′ P is 4 h 2 = 2 7 1 . The other three corners are clearly the same size.
Finally, the area of the octagon in question is 2 7 3 2 − 4 ( 2 7 1 ) = 2 7 2 8 = 3 3 2 2 ⋅ 7 . Thus a = 2 , b = 7 , c = 3 and a + b + c = 1 2